题目内容
如图,在直角坐标系中,点A坐标为(1,0),点B坐标为(0,1),E、F是线段AB上的两个动点,且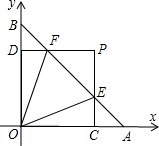 ∠EOF=45°,过点E、F分别作x轴和y轴的垂线CE、DF相交于点P,垂足分别为C、D、设P点的坐标为(x,y),令xy=k,
∠EOF=45°,过点E、F分别作x轴和y轴的垂线CE、DF相交于点P,垂足分别为C、D、设P点的坐标为(x,y),令xy=k,(1)求证:△AOF∽△BEO;
(2)当OC=OD时,求k的值;
(3)在点E、F运动过程中,点P也随之运动,探索:k是否为定值?请证明你的结论.
分析:(1)要证明△AOF∽△BEO,由题意可知OA=OB,∠AOB=90°,∴∠OAF=∠OBE=45°,看边角关系,只要证∠AOF=∠BEO即可∠AOF=∠AOE+∠EOF,∠BEO=∠OAF+∠AOE;∵∠EOF=45°,∴∠AOF=∠BEO.问题得证.
(2)当OC=OD时,作OM⊥AB于M,OM=
AB=
,由OC=OD,OA=OB=1,可以得到CE=DF,又∠OCE=∠ODF,
∴△OCE≌△ODF,故有OF=OE,∠EOM=
∠EOF=22.5°,而∠COE=∠AOM-∠EOM=45°-22.5°=22.5°=∠EOM,
∴PC=PD=OC=
,k值可求.
(3)假设k的值为定值,即PC•PD=定值,作FK⊥OA于点K,EH⊥OB于点H,由△AOF∽△BEO得
=
,∴AF×BE=OA×OB=1,BE=
HE,AF=
FK,于是
HE×
FK=1,即HE×FK=
,PC×PD=EH×FK=
,问题可求.
(2)当OC=OD时,作OM⊥AB于M,OM=
| 1 |
| 2 |
| ||
| 2 |
∴△OCE≌△ODF,故有OF=OE,∠EOM=
| 1 |
| 2 |
∴PC=PD=OC=
| ||
| 2 |
(3)假设k的值为定值,即PC•PD=定值,作FK⊥OA于点K,EH⊥OB于点H,由△AOF∽△BEO得
| AF |
| OB |
| OA |
| BE |
| 2 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:(1)证明:由题意得OA=OB,∠AOB=90°,
∴∠OAF=∠OBE=45°;
又∵∠AOF=∠AOE+∠EOF,∠BEO=∠OAF+∠AOE;∠EOF=45°,
∴∠AOF=∠BEO,
∴△AOF∽△BEO.
(2)解:作OM⊥AB于M,则OM=
AB=
∵OC=OD,OA=OB=1,
∴CE=DF,
又∵∠OCE=∠ODF,
∴△OCE≌△ODF,
∴OF=OE,
∵∠EOM=
∠EOF=22.5°,又∠COE=∠AOM-∠EOM=45°-22.5°=22.5°=∠EOM
∴PC=PD=OC=
,
∴k=PC×PD=
.
(3)解:如图,作FK⊥OA于点K,EH⊥OB于点H,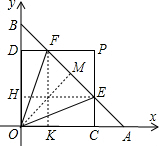
∵△AOF∽△BEO,
∴
=
,
∴AF×BE=OA×OB=1,
∵BE=
HE,AF=
FK,
∴
HE×
FK=1,即HE×FK=
,
∴PC×PD=EH×FK=
,
∴k的值为定值
.
∴∠OAF=∠OBE=45°;
又∵∠AOF=∠AOE+∠EOF,∠BEO=∠OAF+∠AOE;∠EOF=45°,
∴∠AOF=∠BEO,
∴△AOF∽△BEO.
(2)解:作OM⊥AB于M,则OM=
| 1 |
| 2 |
| ||
| 2 |
∵OC=OD,OA=OB=1,
∴CE=DF,
又∵∠OCE=∠ODF,
∴△OCE≌△ODF,
∴OF=OE,
∵∠EOM=
| 1 |
| 2 |
∴PC=PD=OC=
| ||
| 2 |
∴k=PC×PD=
| 1 |
| 2 |
(3)解:如图,作FK⊥OA于点K,EH⊥OB于点H,

∵△AOF∽△BEO,
∴
| AF |
| OB |
| OA |
| BE |
∴AF×BE=OA×OB=1,
∵BE=
| 2 |
| 2 |
∴
| 2 |
| 2 |
| 1 |
| 2 |
∴PC×PD=EH×FK=
| 1 |
| 2 |
∴k的值为定值
| 1 |
| 2 |
点评:本题综合运用了全等、相似三角形的判定和性质,及三角形的内外角关系等,来解题,综合性强,属能力拔高题.

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目

 如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.

 ,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:
,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件: