题目内容
如图,正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG,EF交AD于点H.(1)求证:AH=EH;
(2)若正方形ABCD的边长为3,求DH的长.
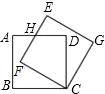
分析:(1)连CH,由正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG,根据旋转的性质得到CF=CD,∠DCG=30°,易证得Rt△CFH≌Rt△CDH,则HF=HD,即可得到结论;
(2)由(1)得Rt△CFH≌Rt△CDH,有∠FCH=∠DCH,而∠DCG=30°,得∠DCF=90°-30°=60°,所以∠DCH=30°,而CD=3,利用含30度的直角三角形三边的关系即可求出DH的长.
(2)由(1)得Rt△CFH≌Rt△CDH,有∠FCH=∠DCH,而∠DCG=30°,得∠DCF=90°-30°=60°,所以∠DCH=30°,而CD=3,利用含30度的直角三角形三边的关系即可求出DH的长.
解答:(1)证明:连CH,如图,
∵正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG,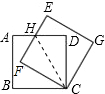
∴CF=CD,∠DCG=30°,
而CH公共,
∴Rt△CFH≌Rt△CDH,
∴HF=HD,
∴AH=HE;
(2)解:由(1)得Rt△CFH≌Rt△CDH,
∴∠FCH=∠DCH,
而∠DCG=30°,
∴∠DCF=90°-30°=60°,
∴∠DCH=30°,
而正方形ABCD的边长为3,即CD=3,
∵在直角三角形中,三边之比为1:
:2.
∴DH=
DC=
.
∵正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG,

∴CF=CD,∠DCG=30°,
而CH公共,
∴Rt△CFH≌Rt△CDH,
∴HF=HD,
∴AH=HE;
(2)解:由(1)得Rt△CFH≌Rt△CDH,
∴∠FCH=∠DCH,
而∠DCG=30°,
∴∠DCF=90°-30°=60°,
∴∠DCH=30°,
而正方形ABCD的边长为3,即CD=3,
∵在直角三角形中,三边之比为1:
| 3 |
∴DH=
| ||
| 3 |
| 3 |
点评:本题考查了旋转的性质:旋转前后的两个图形全等,对应点与旋转中心的连线段的夹角等于旋转角,对应点到旋转中心的距离相等.也考查了直角三角形全等的判定与性质以及含30度的直角三角形三边的关系.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
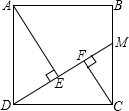 19、如图:正方形ABCD,M是线段BC上一点,且不与B、C重合,AE⊥DM于E,CF⊥DM于F.求证:AE2+CF2=AD2.
19、如图:正方形ABCD,M是线段BC上一点,且不与B、C重合,AE⊥DM于E,CF⊥DM于F.求证:AE2+CF2=AD2.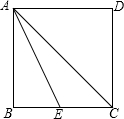 如图,正方形ABCD中,E点在BC上,AE平分∠BAC.若BE=
如图,正方形ABCD中,E点在BC上,AE平分∠BAC.若BE=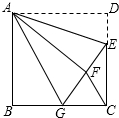 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=3.其中正确结论的个数是( )
如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=3.其中正确结论的个数是( )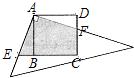 17、如图,正方形ABCD的边长为4,将一个足够大的直角三角板的直角顶点放于点A处,该三角板的两条直角边与CD交于点F,与CB延长线交于点E,四边形AECF的面积是
17、如图,正方形ABCD的边长为4,将一个足够大的直角三角板的直角顶点放于点A处,该三角板的两条直角边与CD交于点F,与CB延长线交于点E,四边形AECF的面积是 如图,正方形ABCD的边CD在正方形ECGF的边CE上,连接BE、DG.
如图,正方形ABCD的边CD在正方形ECGF的边CE上,连接BE、DG.