题目内容
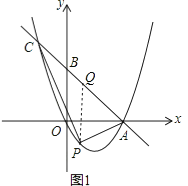
【题目】如图1,已知直线l:y=﹣x+2与x轴交于点A、与y轴交于点B.抛物线y=ax2+bx+c(a≠0)经过O、A两点,与直线l交于点C,点C的横坐标为﹣1.
(1)求该抛物线的函数表达式;
(2)若点P是位于直线l下方抛物线上的一个动点,且不与点A、点C重合,连接PA、PC.设△PAC的面积为S,求当S取得最大值时点P的坐标,并求S的最大值;
(3)如图2,设抛物线的顶点为D,连接AD、BD.点E是对称轴m上一点,F是抛物线上一点,请直接写出当△DEF与△ABD相似时点E的坐标.
【答案】
(1)
解:当x=﹣1时,y=﹣x+2=3,则C(﹣1,3),
当y=0时,﹣x+2=0,解得x=2,则A(2,0),
∵抛物线过点O(0,0)、A(2,0),
设抛物线解析式为y=ax( x﹣2 ),
将点C(﹣1,3)代入得3=﹣a(﹣1﹣2 ),解得a=1,
∴该抛物线解析式为y=x( x﹣2 ),即y=x2﹣2x
(2)
解:设P(m,m2﹣2m),过点P作PQ∥y轴,交直线l于点Q,如图1,则Q(m,﹣m+2),
∴PQ=(﹣m+2 )﹣(m2﹣2m)=﹣m2+m+2,
∴S=S△PQC+S△PQA= ![]() (2+1)PQ=﹣
(2+1)PQ=﹣ ![]() m2+
m2+ ![]() m+3=﹣
m+3=﹣ ![]() (m﹣
(m﹣ ![]() )2+
)2+ ![]() ,
,
∴当m= ![]() 时,S有最大值,最大值为
时,S有最大值,最大值为 ![]() ,
,
把m= ![]() 代入m2﹣2m得m2﹣2m=﹣
代入m2﹣2m得m2﹣2m=﹣ ![]() ,
,
∴P( ![]() ,﹣
,﹣ ![]() )
)
(3)
解:设F点坐标为(t,t2﹣2t),
当x=1时,y=x2﹣2x=﹣1,则D(1,﹣1),当x=0时,y=﹣x+2=2,则B(0,2),
∵AB2=22+22=8,AD2=12+12=2,DB2=12+(2+1)2=10,
∴AB2+AD2=DB2,
∴△ABD为直角三角形,∠BAD=90°,
如图2,
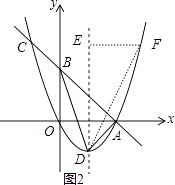
当△DEF∽△BAD,则∠DEF=∠BAD=90°, ![]() =
= ![]() ,即DE:2
,即DE:2 ![]() =EF:
=EF: ![]() ,
,
∴DE=2EF,
∵EF⊥DE,
∴E(1,t2﹣2t),
∴t2﹣2t+1=2(t﹣1),解得t1=1(舍去),t2=3,此时E点坐标为(1,3);
当△DEF∽△DAB,则∠DEF=∠BAD=90°, ![]() =
= ![]() ,即DE:
,即DE: ![]() =EF:2
=EF:2 ![]() ,
,
∴DE= ![]() EF,
EF,
∵EF⊥DE,
∴E(1,t2﹣2t),
∴t2﹣2t+1= ![]() (t﹣1),解得t1=1(舍去),t2=
(t﹣1),解得t1=1(舍去),t2= ![]() ,此时E点坐标为(1,﹣
,此时E点坐标为(1,﹣ ![]() );
);
如图3,
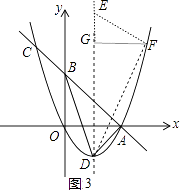
当△DFE∽△BAD,则∠DFE=∠BAD=90°,∠FDE=∠ADB,
过F点作FG⊥DE于G,则△DGF∽△BAD,同样方法可得G(1,3),则F(3,3),
∵GF2=GEGD,即22=GE4,
∴GE=1,
∴此时E点坐标为(1,4);
当△DFE∽△DAB,则∠DFE=∠BAD=90°,用同样方法可得E点坐标为(1, ![]() ),
),
综上所述,E点坐标为(1,3),(1,4),(1, ![]() ),(1,﹣
),(1,﹣ ![]() ).
).
【解析】(1)先根据一次函数图象上点的坐标特征求出C(﹣1,3),A(2,0),再设交点式y=ax( x﹣2 ),然后把点C点坐标代入求出a即可得到该抛物线解析式为y=x2﹣2x;(2)设P(m,m2﹣2m),过点P作PQ∥y轴,交直线l于点Q,如图1,则Q(m,﹣m+2),则PQ=﹣m2+m+2,根据三角形面积公式,利用S=S△PQC+S△PQA可得到S=﹣ ![]() m2+
m2+ ![]() m+3,然后根据二次函数的性质解决最值问题(3)设F点坐标为(t,t2﹣2t),先确定D(1,﹣1),B(0,2),再利用勾股定理的逆定理证明△ABD为直角三角形,∠BAD=90°,然后分类讨论:如图2,当△DEF∽△BAD,则∠DEF=∠BAD=90°,利用相似比得DE=2EF,由于EF⊥DE,则E(1,t2﹣2t),所以t2﹣2t+1=2(t﹣1),解得t1=1(舍去),t2=3,易得此时E点坐标为(1,3);当△DEF∽△DAB,则∠DEF=∠BAD=90°,
m+3,然后根据二次函数的性质解决最值问题(3)设F点坐标为(t,t2﹣2t),先确定D(1,﹣1),B(0,2),再利用勾股定理的逆定理证明△ABD为直角三角形,∠BAD=90°,然后分类讨论:如图2,当△DEF∽△BAD,则∠DEF=∠BAD=90°,利用相似比得DE=2EF,由于EF⊥DE,则E(1,t2﹣2t),所以t2﹣2t+1=2(t﹣1),解得t1=1(舍去),t2=3,易得此时E点坐标为(1,3);当△DEF∽△DAB,则∠DEF=∠BAD=90°, ![]() =
= ![]() ,利用相似比得DE=
,利用相似比得DE= ![]() EF,
EF,
由EF⊥DE得到E(1,t2﹣2t),则t2﹣2t+1= ![]() (t﹣1),解得t1=1(舍去),t2=
(t﹣1),解得t1=1(舍去),t2= ![]() ,易得此时E点坐标为(1,﹣
,易得此时E点坐标为(1,﹣ ![]() );如图3,当△DFE∽△BAD,则∠DFE=∠BAD=90°,∠FDE=∠ADB,过F点作FG⊥DE于G,则△DGF∽△BAD,用前面方法可得G(1,3),则F(3,3),利用GF2=GEGD可计算出GE=1,则此时E点坐标为(1,4);当△DFE∽△DAB,则∠DFE=∠BAD=90°,用同样方法可得E点坐标为(1,
);如图3,当△DFE∽△BAD,则∠DFE=∠BAD=90°,∠FDE=∠ADB,过F点作FG⊥DE于G,则△DGF∽△BAD,用前面方法可得G(1,3),则F(3,3),利用GF2=GEGD可计算出GE=1,则此时E点坐标为(1,4);当△DFE∽△DAB,则∠DFE=∠BAD=90°,用同样方法可得E点坐标为(1, ![]() ).
).
【考点精析】根据题目的已知条件,利用一次函数的性质和二次函数的图象的相关知识可以得到问题的答案,需要掌握一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小;二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点.