ΧβΡΩΡΎ»ί
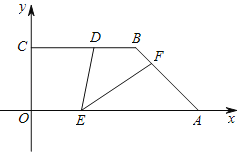
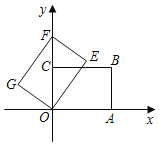
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒxOy÷–Θ§ΨΊ–ΈOABCΒΡΕΞΒψAΓΔC‘ΎΉχ±ξ÷α…œΘ§ΒψAΒΡΉχ±ξΈΣ(4Θ§0)Θ°ΒψCΒΡΉχ±ξΈΣ(0Θ§3)Θ°ΫΪΨΊ–ΈOABC»ΤΒψOΡφ ±’κ–ΐΉΣΒΟΒΫΨΊ–ΈOEFGΘ§ΒψBΒΡΕ‘”ΠΒψF«ΓΚΟ¬δ‘Ύy÷α’ΐΑκ÷α…œΘ°ΫΪΨΊ–ΈOEFG―Ίy÷αœρœ¬ΤΫ“ΤΘ§Β±ΒψEΒΫ¥οx÷α…œ ±Θ§‘ΥΕ·ΆΘ÷ΙΘ°…ηΤΫ“ΤΒΡΨύάκΈΣmΘ§ΝΫΨΊ–Έ÷ΊΒΰΟφΜΐΈΣSΘ°
Θ®1Θ©«σΒψEΒΡΉχ±ξΘΜ
Θ®2Θ©«σS”κmΒΡΚ· ΐΙΊœΒ ΫΘ§≤Δ÷±Ϋ”–¥≥ωmΒΡ»Γ÷ΒΖΕΈßΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©ΒψEΒΡΉχ±ξ![]() ΘΜΘ®2Θ©SΘΫ
ΘΜΘ®2Θ©SΘΫ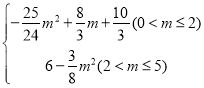
ΓΨΫβΈωΓΩ
Θ®1Θ©ΙΐEΉςEHΓΆx÷α”ΎHΘ§ΗυΨί“―÷ΣΧθΦΰΒΟΒΫOAΘΫ4Θ§OCΘΫ3Θ§ΗυΨί–ΐΉΣΒΡ–‘÷ ΒΟΒΫOEΘΫOAΘΫ4Θ§EFΘΫOCΘΫ3Θ§ΗυΨίΙ¥Ι…Ε®άμΦ¥Ω…ΒΟΒΫΫα¬έΘΜ
Θ®2Θ©Ζ÷ΝΫ÷÷«ιΩωΧ÷¬έΦ¥Ω…Θ°
ΫβΘΚΘ®1Θ©ΙΐEΉςEHΓΆx÷α”ΎHΘ§
ΓΏΒψAΒΡΉχ±ξΈΣΘ®4Θ§0Θ©Θ°ΒψCΒΡΉχ±ξΈΣΘ®0Θ§3Θ©Θ§
ΓύOAΘΫ4Θ§OCΘΫ3Θ§
ΓΏΫΪΨΊ–ΈOABC»ΤΒψOΡφ ±’κ–ΐΉΣΒΟΒΫΨΊ–ΈOEFGΘ§
ΓύOEΘΫOAΘΫ4Θ§EFΘΫOCΘΫ3Θ§
ΓύOFΘΫ![]() ΘΫ5Θ§
ΘΫ5Θ§
ΓύEHΘΫ![]() ΘΫ
ΘΫ![]() Θ§
Θ§
ΓύOHΘΫ![]() ΘΫ
ΘΫ![]() ΘΫ
ΘΫ![]() Θ§
Θ§
ΓύΒψEΒΡΉχ±ξΘΚ![]() ΘΜ
ΘΜ
Θ®2Θ©»γΆΦ2Θ§Β±![]() ‘ΎBC…œΖΫ ±Θ§Φ¥m
‘ΎBC…œΖΫ ±Θ§Φ¥m![]() ±Θ§
±Θ§
![]() Θ§
Θ§
ΓΏ![]()
Γύ![]()
ΓΏ![]()
Γύ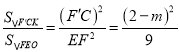 Θ§
Θ§
Γύ![]() Θ§
Θ§
Ά§άμΩ…ΒΟ≥ωΘ§
![]() Θ§
Θ§
Γύ![]() ΘΜ
ΘΜ
»γΆΦΘ®3Θ©Β±![]() ‘ΎœΏΕΈCO…œ ±Θ§Φ¥
‘ΎœΏΕΈCO…œ ±Θ§Φ¥![]() ±Θ§
±Θ§
ΓΏ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
ΓύS=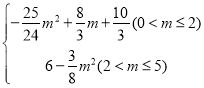 Θ°
Θ°



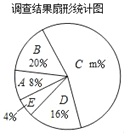
 ΩΣ–ΡΩλά÷ΦΌΤΎΉς“Β νΦΌΉς“ΒΈςΑ≤≥ωΑφ…γœΒΝ–¥πΑΗ
ΩΣ–ΡΩλά÷ΦΌΤΎΉς“Β νΦΌΉς“ΒΈςΑ≤≥ωΑφ…γœΒΝ–¥πΑΗ ΟϊΧβ―ΒΝΖœΒΝ–¥πΑΗ
ΟϊΧβ―ΒΝΖœΒΝ–¥πΑΗΓΨΧβΡΩΓΩ«ΎΦσΫΎ‘Φ“Μ÷± «÷–ΜΣΟώΉεΒΡ¥ΪΆ≥ΟάΒ¬Θ§Ρ≥÷–―ß–ΘΆ≈Έ·ΉΦ±Η“‘ΓΑ«ΎΦσΫΎ‘ΦΓ±ΈΣ÷ςΧβΩΣ’Ι“Μ¥Έ―ίΫ≤±»»ϋΘ§ΈΣ¥Υœ»Ε‘Ά§―ßΟ«ΟΩ‘¬ΝψΜ®«°ΒΡ ΐΕνΫχ––“Μ–©ΝΥΫβΘ§ΥφΜζΒς≤ιΝΥ±Ψ–Θ≤ΩΖ÷Ά§―ßΘ§ΗυΨίΒς≤ιΫαΙϊΘ§Μφ÷Τ≥ωΝΥ»γœ¬ΝΫΗω…–≤ΜΆξ’ϊΒΡΆ≥ΦΤΆΦ±μΘ°
Ήι±π | Ζ÷ΉιΘ®ΒΞΈΜΘΚ‘ΣΘ© | »Υ ΐ |
A | 0ΓήxΘΦ30 | 4 |
B | 30ΓήxΘΦ60 | a |
C | 60ΓήxΘΦ90 | b |
D | 90ΓήxΘΦ120 | 8 |
E | 120ΓήxΘΦ150 | 2 |
ΗυΨί“‘…œΆΦ±μΘ§Ϋβ¥πœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©ΧνΩ’ΘΚ’β¥ΈΒς≤ιΒΡΆ§―ßΙ≤”–ΓΓ ΓΓ»ΥΘ§a+bΘΫΓΓ ΓΓΘ§mΘΫΓΓ ΓΓΘΜ
Θ®2Θ©«σ…»–ΈΆ≥ΦΤΆΦ÷–…»–ΈBΒΡ‘≤–ΡΫ«ΒΡΕ» ΐΘΜ
Θ®3Θ©ΗΟ–ΘΙ≤”–1200Οϊ―ß…ζΘ§«κΙάΦΤΟΩ‘¬ΝψΜ®«°ΒΡ ΐΕν‘Ύ60ΓήxΘΦ90ΖΕΈßΒΡ»Υ ΐΘ°