题目内容
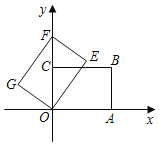
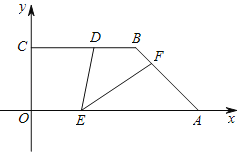
【题目】如图,BC⊥y轴,BC<OA,点A、点C分别在x轴、y轴的正半轴上,D是线段BC上一点,BD=![]() OA=2,AB=3,∠OAB=45°,E、F分别是线段OA、AB上的两动点,且始终保持∠DEF=45°,将△AEF沿一条边翻折,翻折前后两个三角形组成的四边形为菱形,则线段OE的值为_____.
OA=2,AB=3,∠OAB=45°,E、F分别是线段OA、AB上的两动点,且始终保持∠DEF=45°,将△AEF沿一条边翻折,翻折前后两个三角形组成的四边形为菱形,则线段OE的值为_____.
【答案】6﹣![]() 或6或9﹣3
或6或9﹣3![]()
【解析】
可得到∠DOE=∠EAF,∠OED=∠AFE,即可判定△DOE∽△EAF,分情况进行讨论:①当EF=AF时,△AEF沿AE翻折,所得四边形为菱形,进而得到OE的长;②当AE=AF时,△AEF沿EF翻折,所得四边形为菱形,进而得到OE的长;③当AE=EF时,△AEF沿AF翻折,所得四边形为菱形,进而得到OE的长.
解:连接OD,过点BH⊥x轴,
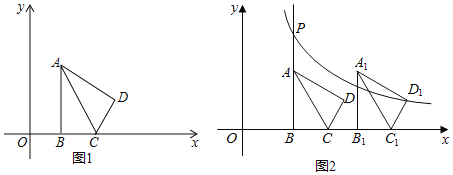
①沿着EA翻折,如图1:∵∠OAB=45°,AB=3,
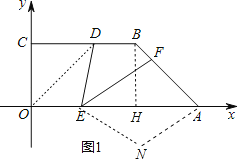
∴AH=BH=ABsin45°=![]() ,
,
∴CO=![]() ,
,
∵BD=![]() OA=2,
OA=2,
∴BD=2,OA=8,
∴BC=8﹣![]() ,
,
∴CD=6﹣![]() ;
;
∵四边形FENA是菱形,
∴∠FAN=90°,
∴四边形EFAN是正方形,
∴△AEF是等腰直角三角形,
∵∠DEF=45°,
∴DE⊥OA,
∴OE=CD=6﹣![]() ;
;
②沿着AF翻折,如图2:
∴AE=EF,
∴B与F重合,
∴∠BDE=45°,
∵四边形ABDE是平行四边形
∴AE=BD=2,
∴OE=OA﹣AE=8﹣2=6;
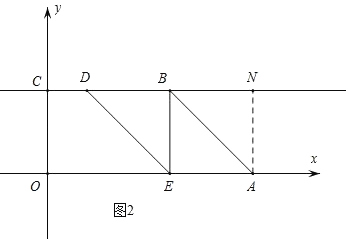
③沿着EF翻折,如图3:

∴AE=AF,
∵∠EAF=45°,
∴△AEF是等腰三角形,
过点F作FM⊥x轴,过点D作DN⊥x轴,
∴△EFM∽△DNE,
∴![]() ,
,
∴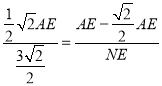 ,
,
∴NE=3﹣![]() ,
,
∴OE=6﹣![]() +3﹣
+3﹣![]() =9﹣3
=9﹣3![]() ;
;
综上所述:OE的长为6﹣![]() 或6或9﹣3
或6或9﹣3![]() ,
,
故答案为6﹣![]() 或6或9﹣3
或6或9﹣3![]() .
.

 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案【题目】交通工程学理论把在单向道路上行驶的汽车看成连续的流体,并用流量、速度、密度三个概念描述车流的基本特征,其中流量![]() (辆
(辆![]() 小时)指单位时间内通过道路指定断面的车辆数;速度
小时)指单位时间内通过道路指定断面的车辆数;速度![]() (千米
(千米![]() 小时)指通过道路指定断面的车辆速度,密度
小时)指通过道路指定断面的车辆速度,密度![]() (辆
(辆![]() 千米)指通过道路指定断面单位长度内的车辆数.为配合大数据治堵行动,测得某路段流量
千米)指通过道路指定断面单位长度内的车辆数.为配合大数据治堵行动,测得某路段流量![]() 与速度
与速度![]() 之间关系的部分数据如下表:
之间关系的部分数据如下表:
速度v(千米/小时) |
|
|
|
|
|
|
|
|
流量q(辆/小时) |
|
|
|
|
|
|
|
|
(1)根据上表信息,下列三个函数关系式中,刻画![]() ,
,![]() 关系最准确是_____________________.(只填上正确答案的序号)
关系最准确是_____________________.(只填上正确答案的序号)
①![]() ;②
;②![]() ;③
;③![]()
(2)请利用(1)中选取的函数关系式分析,当该路段的车流速度为多少时,流量达到最大?最大流量是多少?
(3)已知![]() ,
,![]() ,
,![]() 满足
满足![]() ,请结合(1)中选取的函数关系式继续解决下列问题:市交通运行监控平台显示,当
,请结合(1)中选取的函数关系式继续解决下列问题:市交通运行监控平台显示,当![]() 时道路出现轻度拥堵.试分析当车流密度
时道路出现轻度拥堵.试分析当车流密度![]() 在什么范围时,该路段将出现轻度拥堵?
在什么范围时,该路段将出现轻度拥堵?