题目内容
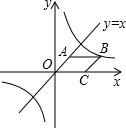 如图所示,已知菱形OABC,点C在x轴上,直线y=x经过点A,菱形OABC的面积是
如图所示,已知菱形OABC,点C在x轴上,直线y=x经过点A,菱形OABC的面积是| 2 |
分析:首先根据直线y=x经过点A,设A点坐标为(a,a),再利用勾股定理算出AO=
a,由菱形的性质可得到AO=CO=CB=AB=
a,再利用菱形的面积公式计算出a的值,进而得到A点坐标,则可求得B点坐标,再利用待定系数法求出反比例函数表达式.
| 2 |
| 2 |
解答:解:∵直线y=x经过点A,
∴设A(a,a),
∴OA2=a2+a2=2a2,
∴AO=
a,
∵四边形ABCD是菱形,
∴AO=CO=CB=AB=
a,
∵菱形OABC的面积是
,
∴
a•a=
,
解得:a=1,
∴AB=
,A(1,1)
∴B(
+1,1),
设反比例函数解析式为y=
(k≠0),
∵反比例函数的图象经过点B,
∴k=(
+1)×1=
+1,
∴反比例函数解析式为y=
,
故选C.
∴设A(a,a),
∴OA2=a2+a2=2a2,
∴AO=
| 2 |
∵四边形ABCD是菱形,
∴AO=CO=CB=AB=
| 2 |
∵菱形OABC的面积是
| 2 |
∴
| 2 |
| 2 |
解得:a=1,
∴AB=
| 2 |
∴B(
| 2 |
设反比例函数解析式为y=
| k |
| x |
∵反比例函数的图象经过点B,
∴k=(
| 2 |
| 2 |
∴反比例函数解析式为y=
| ||
| x |
故选C.
点评:此题主要考查了待定系数法求反比例函数的解析式、菱形的面积公式以及菱形的性质.解题的关键是根据菱形的面积求出A点坐标,进而得到B点坐标,即可算出反比例函数解析式;注意方程思想与数形结合思想的应用.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
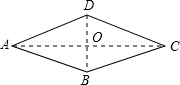 如图所示.已知菱形的边长为10
如图所示.已知菱形的边长为10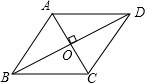
 (2013•本溪一模)如图所示,已知菱形ABCD的对角线AC,BD的长分别为12cm,16cm,AE⊥BC于点E,则AE的长是( )
(2013•本溪一模)如图所示,已知菱形ABCD的对角线AC,BD的长分别为12cm,16cm,AE⊥BC于点E,则AE的长是( ) 如图所示,已知菱形ABCD的一条对角线BD上一点O,到菱形一边AB的距离为2,那么点O到( )
如图所示,已知菱形ABCD的一条对角线BD上一点O,到菱形一边AB的距离为2,那么点O到( )