题目内容
如图所示,已知菱形ABCD的边长为2cm,∠BAD=120°,对角线AC,BD交于点O,则这个菱形的对角线长为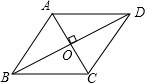
分析:已知边长及∠BAD=120°,不难求出∠ABC的度数为60°,从而进一步求得△ABC为正三角形,从而求得AC及BO的长,于是再利用菱形的面积公式求得面积.
解答:解:∵菱形ABCD∠BAD=120°,AB=BC
∴△ABC为正三角形,
∴AC=AB=2cm.
∵四边形ABCD是菱形
∴AC⊥BD,∠BAO=
∠BAD=
×120°=60°
在Rt△AOB中,
∵∠ABO=90°-∠BAO=30°
∴AO=
AB=1,BO=
=
,
∵AO=
AC,BO=
BD
∴AC=2AO=2,BD=2BO=2
∴S菱形ABCD=
AC•BD=2
∴△ABC为正三角形,
∴AC=AB=2cm.
∵四边形ABCD是菱形
∴AC⊥BD,∠BAO=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△AOB中,
∵∠ABO=90°-∠BAO=30°
∴AO=
| 1 |
| 2 |
| AB2-AO2 |
| 3 |
∵AO=
| 1 |
| 2 |
| 1 |
| 2 |
∴AC=2AO=2,BD=2BO=2
| 3 |
∴S菱形ABCD=
| 1 |
| 2 |
| 3 |
点评:本题主要利用菱形的对角线互相垂直平分及勾股定理来解决.

练习册系列答案
相关题目
 如图所示.已知菱形的边长为10
如图所示.已知菱形的边长为10 (2013•本溪一模)如图所示,已知菱形ABCD的对角线AC,BD的长分别为12cm,16cm,AE⊥BC于点E,则AE的长是( )
(2013•本溪一模)如图所示,已知菱形ABCD的对角线AC,BD的长分别为12cm,16cm,AE⊥BC于点E,则AE的长是( ) 如图所示,已知菱形ABCD的一条对角线BD上一点O,到菱形一边AB的距离为2,那么点O到( )
如图所示,已知菱形ABCD的一条对角线BD上一点O,到菱形一边AB的距离为2,那么点O到( )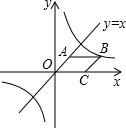 如图所示,已知菱形OABC,点C在x轴上,直线y=x经过点A,菱形OABC的面积是
如图所示,已知菱形OABC,点C在x轴上,直线y=x经过点A,菱形OABC的面积是