题目内容
 (2013•本溪一模)如图所示,已知菱形ABCD的对角线AC,BD的长分别为12cm,16cm,AE⊥BC于点E,则AE的长是( )
(2013•本溪一模)如图所示,已知菱形ABCD的对角线AC,BD的长分别为12cm,16cm,AE⊥BC于点E,则AE的长是( )分析:由菱形ABCD的对角线AC,BD的长分别为12cm,16cm,可求得边BC的长与其面积,又由S菱形ABCD=BC•AE,即可求得答案.
解答:解:∵四边形ABCD是菱形,且AC=12cm,BD=16cm,
∴OB=
BD=8cm,OC=
AC=6cm,AC⊥BD,
∴BC=
=10(cm),
∵S菱形ABCD=
AC•BD=
×12×16=96(cm2),S菱形ABCD=BC•AE=10AE,
∴AE=
=
(cm).
故选D.
∴OB=
| 1 |
| 2 |
| 1 |
| 2 |
∴BC=
| OB2+OC2 |
∵S菱形ABCD=
| 1 |
| 2 |
| 1 |
| 2 |
∴AE=
| 96 |
| 10 |
| 48 |
| 5 |
故选D.
点评:此题考查了菱形的性质以及勾股定理.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
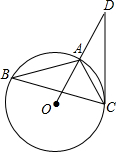 (2013•本溪一模)如图,已知:△ABC是的⊙O内接三角形,D是OA延长线上的一点,连接DC,且∠B=∠D=30°.
(2013•本溪一模)如图,已知:△ABC是的⊙O内接三角形,D是OA延长线上的一点,连接DC,且∠B=∠D=30°.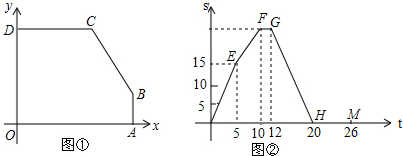
 (2013•本溪一模)如图,已知抛物线y=ax2+bx+3(a≠0)经过A(-1,0),C(3,0)两点.
(2013•本溪一模)如图,已知抛物线y=ax2+bx+3(a≠0)经过A(-1,0),C(3,0)两点.