题目内容
下列结论正确的是
- A.-2与2互为倒数
- B.-2＜0
- C.
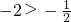
- D.-2与
互为相反数
B
分析：从互为倒数的定义入手，可判断出A是否正确，根据任何负数都小于0得出B的正确性，根据负数的比较大小方法，绝对值大的反而小，判断出C，根据互为相反数的定义，判断出D．
解答：A．-2与2互为倒数，从互为倒数的定义入手，两数数相乘等于1，而-2×2=-4，故选项A错误；
B．-2＜0，根据任何负数都小于0，直接得出答案，故选项B正确；
C．-2＞-
，根据负数的比较大小方法，绝对值大的反而小，可以得出，|-2|＞||，故-2＜-，故选项C错误；
D．-2与互为相反数，根据互为相反数的定义，即和为0，-2+（-）=
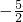≠0，故选项D错误．
故选：B．
点评：此题主要考查了有理数大小的比较以及互为相反数和互为倒数的定义，题目难度不大，关键是区分这几个定义．
分析：从互为倒数的定义入手，可判断出A是否正确，根据任何负数都小于0得出B的正确性，根据负数的比较大小方法，绝对值大的反而小，判断出C，根据互为相反数的定义，判断出D．
解答：A．-2与2互为倒数，从互为倒数的定义入手，两数数相乘等于1，而-2×2=-4，故选项A错误；
B．-2＜0，根据任何负数都小于0，直接得出答案，故选项B正确；
C．-2＞-
，根据负数的比较大小方法，绝对值大的反而小，可以得出，|-2|＞||，故-2＜-，故选项C错误；D．-2与
互为相反数，根据互为相反数的定义，即和为0，-2+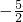（-）=≠0，故选项D错误．故选：B．
点评：此题主要考查了有理数大小的比较以及互为相反数和互为倒数的定义，题目难度不大，关键是区分这几个定义．
练习册系列答案
相关题目
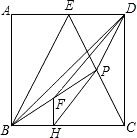如图，已知边长为4的正方形ABCD中，E为AD中点，P为CE中点，F为BP中点，FH⊥BC交BC于H，连接PH，则下列结论正确的是（ ）①BE=CE；②sin∠EBP=
| 1 |
| 2 |
| A、①④⑤ | B、①②③ |
| C、①②④ | D、①③④ |
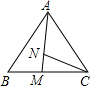如图，点M在BC上，点N在AM上，CM=CN，| AM |
| AN |
| BM |
| CM |
| A、△ABM∽△ACB |
| B、△ANC∽△AMB |
| C、△ANC∽△ACM |
| D、△CMN∽△BCA |
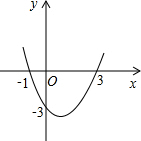已知二次函数y=ax2+bx+c的图象如图所示，则下列结论正确的是（ ）
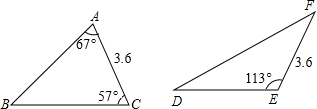如图，△ABC中BC边上的高为h1，AB边上的高为h2，△DEF中DE边上的高为h3，下列结论正确的是（ ）