题目内容
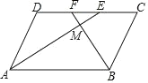
【题目】如图,在□ABCD 中,AE、BF 分别平分∠DAB 和∠ABC,交 CD 于点 E、F,AE、BF 相交于点 M.则线段 DF _______ CE (填>,<或=).
【答案】=
【解析】
DF= CE,利用平行四边形的对边平行,以及角平分线的性质,可以得到△ADE和△BCF都是等腰三角形,那么就有CF=BC=AD=DE,再利用等量减等量差相等,可证.
DF=CE,理由如下:
∵在ABCD中,CD∥AB,
∴∠DEA=∠EAB,
又∵AE平分∠DAB,
∴∠DAE=∠EAB,
∴∠DEA=∠DAE,
∴DE=AD,
同理可得,CF=BC,
又∵在ABCD中,AD=BC,
∴DE=CF,
∴DEEF=CFEF,
即DF=CE.
故答案为:=.

练习册系列答案
相关题目