题目内容
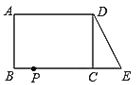
【题目】已知,如图:正方形ABCD,将Rt△EFG斜边EG的中点与点A重合,直角顶点F落在正方形的AB边上,Rt△EFG的两直角边分别交AB、AD边于P、Q两点,(点P与点F重合),如图1所示:



(1)求证:EP2+GQ2=PQ2;
(2)若将Rt△EFG绕着点A逆时针旋转α(0°<α≤90°),两直角边分别交AB、AD边于P、Q两点,如图2所示:判断四条线段EP、PF、FQ、QG之间是否存在什么确定的相等关系?若存在,证明你的结论.若不存在,请说明理由;
(3)若将Rt△EFG绕着点A逆时针旋转α(90°<α<180°),两直角边所在的直线分别交BA、AD两边延长线于P、Q两点,并判断四条线段EP、PF、FQ、QG之间存在何种确定的相等关系?按题意完善图3,请直接写出你的结论(不用证明).
【答案】(1)见解析;(2)PF2+FQ2=EP2+GQ2;(3)四条线段EP、PF、FQ、QG之间的关系为PF2+GQ2=PE2+FQ2.
【解析】
(1)过点E作EH∥FG,由此可证△EAH≌△GAQ,然后根据全等三角形的性质得到EH=QG,又PQ=PH,在Rt△EPH中,EP2+EH2=PH2,由此可以得到EP2+GQ2=PQ2;
(2)过点E作EH∥FG,交DA的延长线于点H,连接PQ、PH,由此可证△EAH≌△GAQ,然后根据全等三角形的性质得到EH=QG,又PH=PQ,在Rt△EPH中,EP2+EH2=PH2,即EP2+GQ2=PH2,在Rt△PFQ中,PF2+FQ2=PQ2,故PF2+FQ2=EP2+GQ2;
(3)四条线段EP、PF、FQ、QG之间的关系为PE2+GQ2=PF2+FQ2,证明方法同上.
(1)过点E作EH∥FG,连接AH、FH,如图所示:
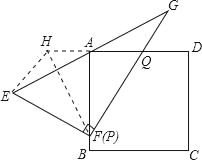
∵EA=AG,∠HEA=∠AGQ,∠HAE=∠GAD,
∴△EAH≌△GAQ,
∴EH=QG,HA=AQ,
∵FA⊥AD,
∴PQ=PH.
在Rt△EPH中,
∵EP2+EH2=PH2,
∴EP2+GQ2=PQ2;
(2)过点E作EH∥FG,交DA的延长线于点H,连接PQ、PH,
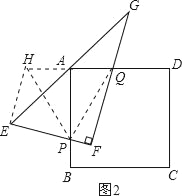
∵EA=AG,∠HEA=∠AGQ,∠HAE=∠GAD,
∴△EAH≌△GAQ,
∴EH=QG,HA=AQ,
∵PA⊥AD,
∴PQ=PH.
在Rt△EPH中,
∵EP2+EH2=PH2,
∴EP2+GQ2=PH2.
在Rt△PFQ中,
∵PF2+FQ2=PQ2,
∴PF2+FQ2=EP2+GQ2.
(3)四条线段EP、PF、FQ、QG之间的关系为PF2+GQ2=PE2+FQ2.