题目内容
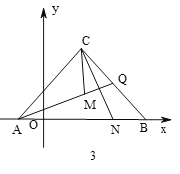
【题目】如图,AB=AC=8,∠BAC=90,直线l与以AB为直径的⊙O相切于点B,点D是直线l上任意一动点,连结DA交⊙O点E.
(1)当点D在AB上方且BD=6时,求AE的长;
(2)当CE恰好与⊙O相切时,求BD的长为多少?

【答案】(1)AE=![]() ;(2)BD= 4.
;(2)BD= 4.
【解析】
(1)连接BE,在Rt△ABD中,利用勾股定理求出AD的长,进而利用直角三角形等面积求出BE的长,在Rt△ABE中,利用勾股定理即可求出AE的长。
(2)连接OC,证明△ABD≌△CAO,根据全等三角形的性质即可求出BD的长.
解:(1)∵AB为直径,
∴∠AEB=90°,
∵BD为切线,
∴AB⊥BD,
∴∠ABD=90°,
在Rt△ABD中, ![]()
∵![]()
∴![]()
在Rt△ABE中, ![]()
(2)连接OC,如图,
∵∠BAC=90°,
∴CA为⊙O的切线,
∵CE为⊙O的切线,
∴CA=CE,
而OA=OE,
∴OC垂直平分AE,
∴∠1+∠3=90°,
而∠1+∠2=90°,
∴∠2=∠3,
而AB=CA,∠CAO=∠ABD,
∴△ABD≌△CAO,
∴BD=AO=4.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
【题目】某公司实行年工资制,职工的年工资由基础工资、住房补贴和医疗费三项组成,具体规定如下:
项目 | 第一年的工资(万元) | 一年后的计算方法 |
基础工资 | 1 | 每年的增长率相同 |
住房补贴 | 0.04 | 每年增加0.04 |
医疗费 | 0.1384 | 固定不变 |
(1)设基础工资每年增长率为x,用含x的代数式表示第三年的基础工资为 万元;
(2)某人在公司工作了3年,他算了一下这3年拿到的住房补贴和医疗费正好是这3年基础工资总额的18 %,问基础工资每年的增长率是多少?