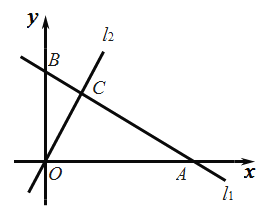题目内容
【题目】在△OAB,△OCD中,OA=OB,OC=OD,∠AOB=∠COD=90°.
(1)若O、C、A在一条直线上,连AD、BC,分别取AD、BC的中点M、N如图(1),求出线段MN、AC之间的数量关系;
(2)若将△OCD绕O旋转到如图(2)的位置,连AD、BC,取BC的中点M,请探究线段OM、AD之间的关系,并证明你的结论;
(3)若将△OCD由图(1)的位置绕O顺时针旋转角度α(0°<α<360°),且OA=4,OC=2,是否存在角度α使得OC⊥BC?若存在,请直接写出此时△ABC的面积;若不存在,请说明理由.

【答案】(1)MN=![]() AC.(2)OM=
AC.(2)OM=![]() AD,OM⊥AD.详见解析;(3)6+2
AD,OM⊥AD.详见解析;(3)6+2![]() 或6﹣2
或6﹣2![]() .
.
【解析】
(1)如图1中,作BH⊥OB,AH⊥OA,连接OM延长OM交BH于P,连接ON延长ON交AH于Q,连接PQ.只要证明MN是△OPQ的中位线,AC=HQ=HP即可解决问题;
(2)结论:OM=![]() AD,OM⊥AD.如图2中,延长OM到H,使得MH=OM,设AD交OH于G,交OB于K.想办法证明△OBH≌△AOD即可解决问题;
AD,OM⊥AD.如图2中,延长OM到H,使得MH=OM,设AD交OH于G,交OB于K.想办法证明△OBH≌△AOD即可解决问题;
(3)分两种情形①如图3中,当OC⊥BC设,作CH⊥OAY于H.S△ABC=S△AOB-S△AOC-S△BOC计算即可;
(1)如图1中,作BH⊥OB,AH⊥OA,连接OM延长OM交BH于P,连接ON延长ON交AH于Q,连接PQ.

∵OA=OB,∠AOB=∠OAH=∠OBH=90°,
∴四边形OAHB是正方形,
∵CM=MB,
∴OM=MB,
∴∠MBO=∠MOB,
∵∠MBO+∠MBP=90°,∠MOB+∠MPB=90°,
∴∠MBP=∠MPB,
∴BM=PM=OM,
同理可证ON=NQ,
∴MN=![]() PQ,
PQ,
∵MC=MB,MO=MP,∠CMO=∠PMB,
∴△CMO≌△BMP,
∴PB=OC,同理可证AQ=OD,
∵OC=OD,
∴AQ=PB=OC=OD,
∵OA=OB=AH=BH,
∴AC=BD=PH=QH,
∵PQ=![]() PH=
PH=![]() AC,
AC,
∴MN=![]() AC.
AC.
(2)结论:OM=![]() AD,OM⊥AD.
AD,OM⊥AD.
理由:如图2中,延长OM到H,使得MH=OM,设AD交OH于G,交OB于K.
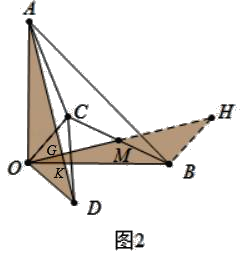
∵CM=BM,∠CMO=∠BMH,OM=MH,
∴△CMO≌△BMH,
∴OC=BH=OD,∠COM=∠H,
∴OC∥BH,
∴∠OBH+∠COB=180°,
∵∠AOD+∠COB=180°,
∴∠OBH=∠AOD,
∵OB=OA,
∴△OBH≌△AOD,
∴AD=OH,∠OAD=∠BOH,
∵∠OAD+∠AKO=90°,
∴∠BOH+∠AKO=90°,
∴∠OGK=90°,
∴AD⊥OH,
∴OM=![]() AD,OM⊥AD.
AD,OM⊥AD.
(3)①如图3中,当OC⊥BC设,作CH⊥OAY于H.
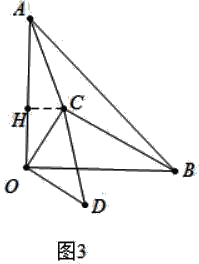
∵∠OCB=90°,OB=2OC,
∴∠OBC=30°,∠OCB=60°,∠COH=30°,
∴CH=![]() OC=1,BC=
OC=1,BC=![]() OC=2
OC=2![]() ,
,
∴S△ABC=S△AOB﹣S△AOC﹣S△BOC=6﹣2![]() .
.
②如图4中,作CH⊥AO于H.

易知∠BOC=60°,∠COH=30°,可得CH=1,BC=2![]() ,
,
∴S△ABC=S△AOB+S△BOC﹣S△AOC=6+2![]() ,
,
综上所述,△ABC的面积为6+2![]() 或6﹣2
或6﹣2![]() .
.