题目内容
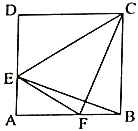
【题目】已知,在菱形ABCD中,∠ADC=60°,点H为CD上任意一点(不与C、D重合),过点H作CD的垂线,交BD于点E,连接AE.
(1)如图1,线段EH、CH、AE之间的数量关系是 ;
(2)如图2,将△DHE绕点D顺时针旋转,当点E、H、C在一条直线上时,求证:AE+EH=CH.
【答案】(1) EH2+CH2=AE2;(2)见解析.
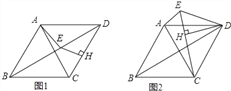
【解析】分析:(1)如图1,过E作EM⊥AD于M,由四边形ABCD是菱形,得到AD=CD,∠ADE=∠CDE,通过△DME≌△DHE,根据全等三角形的性质得到EM=EH,DM=DH,等量代换得到AM=CH,根据勾股定理即可得到结论;
(2)如图2,根据菱形的性质得到∠BDC=∠BDA=30°,DA=DC,在CH上截取HG,使HG=EH,推出△DEG是等边三角形,由等边三角形的性质得到∠EDG=60°,推出△DAE≌△DCG,根据全等三角形的性质即可得到结论.
详解:
(1)EH2+CH2=AE2,
如图1,过E作EM⊥AD于M,
∵四边形ABCD是菱形,
∴AD=CD,∠ADE=∠CDE,
∵EH⊥CD,
∴∠DME=∠DHE=90°,
在△DME与△DHE中,
 ,
,
∴△DME≌△DHE,
∴EM=EH,DM=DH,
∴AM=CH,
在Rt△AME中,AE2=AM2+EM2,
∴AE2=EH2+CH2;
故答案为:EH2+CH2=AE2;
(2)如图2,
∵菱形ABCD,∠ADC=60°,
∴∠BDC=∠BDA=30°,DA=DC,
∵EH⊥CD,
∴∠DEH=60°,
在CH上截取HG,使HG=EH,
∵DH⊥EG,∴ED=DG,
又∵∠DEG=60°,
∴△DEG是等边三角形,
∴∠EDG=60°,
∵∠EDG=∠ADC=60°,
∴∠EDG﹣∠ADG=∠ADC﹣∠ADG,
∴∠ADE=∠CDG,
在△DAE与△DCG中,
 ,
,
∴△DAE≌△DCG,
∴AE=GC,
∵CH=CG+GH,
∴CH=AE+EH.



 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案