题目内容
 如图,AB为⊙O直径,CD为弦,且CD⊥AB,垂足为H.
如图,AB为⊙O直径,CD为弦,且CD⊥AB,垂足为H.(1)∠OCD的平分线CE交⊙O于E,连接OE.求证:E为弧ADB的中点;
(2)如果⊙O的半径为1,CD=
| 3 |
分析:(1)先证明OE∥CD,从而得到OE⊥AB,则OE平分AB所对的弧.
(2)由OC,CD的长度得到∠COB=60°,然后过O作AC的垂线段OF,利用特殊角的三角函数值可求出OF.
(2)由OC,CD的长度得到∠COB=60°,然后过O作AC的垂线段OF,利用特殊角的三角函数值可求出OF.
解答: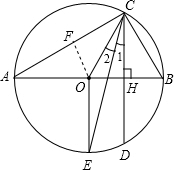 (1)证明:过O作AC的垂线段OF.如图,
(1)证明:过O作AC的垂线段OF.如图,
∵∠OCD的平分线CE交⊙O于E,
∴∠1=∠2.
又∵∠2=∠E,
∴∠E=∠1.
∴OE∥CD,而CD⊥AB.
∴OE⊥AB.
∴OE平分ADB弧,
即E为弧ADB的中点.
(2)解:∵CD=
,
∴CH=
,而OC=1.
∴∠COH=60°.
∴∠A=30°.
∴OF=
OA=
.
即O到弦AC的距离为
.
 (1)证明:过O作AC的垂线段OF.如图,
(1)证明:过O作AC的垂线段OF.如图,∵∠OCD的平分线CE交⊙O于E,
∴∠1=∠2.
又∵∠2=∠E,
∴∠E=∠1.
∴OE∥CD,而CD⊥AB.
∴OE⊥AB.
∴OE平分ADB弧,
即E为弧ADB的中点.
(2)解:∵CD=
| 3 |
∴CH=
| ||
| 2 |
∴∠COH=60°.
∴∠A=30°.
∴OF=
| 1 |
| 2 |
| 1 |
| 2 |
即O到弦AC的距离为
| 1 |
| 2 |
点评:熟练掌握垂径定理及其推论.记住含30度角的直角三角形三边之间的数量关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 6、如图,AB为直径,∠BED=40°,则∠ACD=( )
6、如图,AB为直径,∠BED=40°,则∠ACD=( )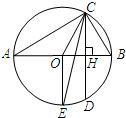 如图,AB为⊙O直径,CD为弦,且CD⊥AB,垂足为H.
如图,AB为⊙O直径,CD为弦,且CD⊥AB,垂足为H.
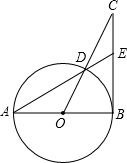 如图,AB为⊙O直径,BC切⊙O于B,CO交⊙O交于D,AD的延长线交BC于E,若∠C=25°,求∠A的度数.
如图,AB为⊙O直径,BC切⊙O于B,CO交⊙O交于D,AD的延长线交BC于E,若∠C=25°,求∠A的度数. 如图,AB为⊙O直径,BC切⊙O于B,CO交⊙O交于D,AD的延长线交BC于E,若∠C=20°,求∠A的度数.
如图,AB为⊙O直径,BC切⊙O于B,CO交⊙O交于D,AD的延长线交BC于E,若∠C=20°,求∠A的度数. 如图,AB为⊙O直径,BC与半径OD垂直于点C,∠B=28°,则∠A的度数为
如图,AB为⊙O直径,BC与半径OD垂直于点C,∠B=28°,则∠A的度数为