题目内容
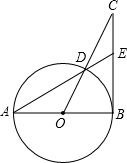 如图,AB为⊙O直径,BC切⊙O于B,CO交⊙O交于D,AD的延长线交BC于E,若∠C=25°,求∠A的度数.
如图,AB为⊙O直径,BC切⊙O于B,CO交⊙O交于D,AD的延长线交BC于E,若∠C=25°,求∠A的度数.
分析:根据切线的性质知:AB⊥BC,根据∠C的度数,可将∠BOC的度数求出;再根据同弧所对的圆周角是圆心角的一半,可得:∠A的度数.
解答:解:∵AB为⊙O的直径,BC切⊙O于B,
∴∠ABC=90°,
∵∠C=25°,
∴∠BOC=65°,
∵∠A=
∠BOD,
∴∠A=32.5°.
∴∠ABC=90°,
∵∠C=25°,
∴∠BOC=65°,
∵∠A=
| 1 |
| 2 |
∴∠A=32.5°.
点评:本题主要考查切线的性质和圆周角定理的应用.

练习册系列答案
相关题目
 6、如图,AB为直径,∠BED=40°,则∠ACD=( )
6、如图,AB为直径,∠BED=40°,则∠ACD=( )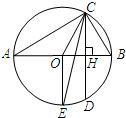 如图,AB为⊙O直径,CD为弦,且CD⊥AB,垂足为H.
如图,AB为⊙O直径,CD为弦,且CD⊥AB,垂足为H.
 如图,AB为⊙O直径,BC切⊙O于B,CO交⊙O交于D,AD的延长线交BC于E,若∠C=20°,求∠A的度数.
如图,AB为⊙O直径,BC切⊙O于B,CO交⊙O交于D,AD的延长线交BC于E,若∠C=20°,求∠A的度数. 如图,AB为⊙O直径,BC与半径OD垂直于点C,∠B=28°,则∠A的度数为
如图,AB为⊙O直径,BC与半径OD垂直于点C,∠B=28°,则∠A的度数为