题目内容
【题目】如图,在△ABC中,∠C=90°,∠CAD=∠BAD,DE⊥AB于E,点F在边AC上,连接DF.
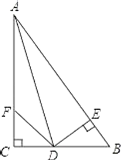
(1)求证:AC=AE;
(2)若CF=BE,直接写出线段AB,AF,EB的数量关系: .
(3)若AC=8,AB=10,且△ABC的面积等于24,求DE的长.
【答案】(1)见解析;(2)AB=AF+2EB;(3)![]() .
.
【解析】
(1)由DE⊥AB,那么∠AED=90°,利用AAS可证△ACD≌△AED,由全等三角形的性质即可得出AC=AE;
(2)由AC=AE,CF=BE,根据AB=AE+EB,AC=AF+CF即可得出结论;
(3)求出△ABC的面积,由△ACD≌△AED,证得DC=DE,然后根据S△ABC=S△ACD+S△ADB即可求得DE.
(1)证明:∵∠C=90°,DE⊥AB,
∴∠C=∠AED=90°,
在△ACD和△AED中,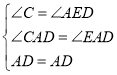 ,
,
∴△ACD≌△AED(AAS),
∴AC=AE;
(2)解:∵AB=AE+EB,AC=AE,
∴AB=AC+EB,
∵AC=AF+CF,CF=BE
∴AC=AF+BE,
∴AB=AF+2EB.
故答案为:AB=AF+2EB;
(3)解:)∵∠C=90°,AC=8,AB=10,
∴BC=![]() = 6,
= 6,
∴S△ABC=![]() ACBC= 24,
ACBC= 24,
由(1)得:△ACD≌△AED,
∴DC=DE,
∵S△ABC=S△ACD+S△ADB,
∴S△ABC=![]() ACCD+
ACCD+![]() ABDE,
ABDE,
又∵AC=8,AB=10,
∴24=![]() ×8×CD+
×8×CD+![]() ×10 ×DE
×10 ×DE
∴DE=![]() .
.

练习册系列答案
相关题目