题目内容
【题目】如图,在边长为12cm的等边三角形ABC中,点P从点A开始沿AB边向点B以每秒钟1cm的速度移动,点Q从点B开始沿BC边向点C以每秒钟2cm的速度移动。若P、Q分别从A、B同时出发,其中任意一点到达目的地后,两点同时停止运动,求: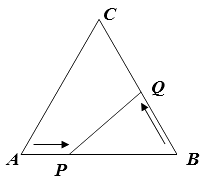
(1)经过6秒后,BP= cm,BQ=cm;
(2)经过几秒后,△BPQ是直角三角形?
(3)经过几秒△BPQ的面积等于 ![]() cm2 ?
cm2 ?
【答案】
(1)6;12
(2)
∵△ABC是等边三角形,
∴AB=AC=12cm,∠A=∠B=∠C=60°,
当∠PQB=90°时,
∴∠BPQ=30°,
∴BP=2BQ
∵BP=12-x,BQ=2x,
∴12-x=2×2x,
∴ ![]()
当∠QPB=90°时,
∴∠PQB=30°,
∴BQ=2PB,
∴2x=2(12-x),
x=6
答:6秒或 ![]() 秒时,△BPQ是直角三角形;
秒时,△BPQ是直角三角形;
(3)
作QD⊥AB于D,
∴∠QDB=90°,
∴∠DQB=30°,
∴DB =0.5 BQ=x,
在Rt△DBQ中,由勾股定理,得
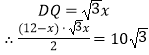
解得;x1=10,x2=2,
∵x=10时,2x>12,故舍去
∴x=2.
答:经过2秒△BPQ的面积等于 ![]() cm2
cm2
【解析】(1)解:由题意,得
AP=6cm,BQ=12cm.
∵△ABC是等边三角形
∴AB=BC=12cm,
∴BP=12-6=6cm.
【考点精析】根据题目的已知条件,利用等边三角形的性质和勾股定理的概念的相关知识可以得到问题的答案,需要掌握等边三角形的三个角都相等并且每个角都是60°;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.

练习册系列答案
相关题目