题目内容
【题目】如图，定点A（﹣2，0），动点B在直线y=x上运动，当线段AB最短时，点B的坐标为 ．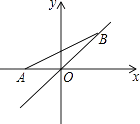 
【答案】（﹣1,﹣1）
【解析】解：过A作AD⊥直线y=x，过D作DE⊥x轴于E，
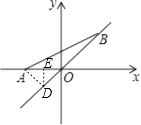
则∠DOA=∠OAD=∠EDO=∠EDA=45°，
∵A（﹣2，0），
∴OA=2，
∴OE=DE=1，
∴D的坐标为（﹣1，﹣1），
即动点B在直线y=x上运动，当线段AB最短时，点B的坐标为（﹣1，﹣1），
所以答案是：（﹣1，﹣1）．
【考点精析】解答此题的关键在于理解正比例函数的图象和性质的相关知识，掌握正比函数图直线，经过一定过原点．K正一三负二四，变化趋势记心间．K正左低右边高，同大同小向爬山．K负左高右边低，一大另小下山峦，以及对等腰三角形的性质的理解，了解等腰三角形的两个底角相等（简称：等边对等角）．
练习册系列答案
相关题目
【题目】青山化工厂与A、B两地有公路、铁路相连，这家工厂从A地购买一批每吨1000元的原料经铁路120km和公路10km运回工厂，制成每吨8000元的产品经铁路110km和公路20km销售到B地．已知铁路的运价为1.2元/（吨·千米)，公路的运价为1.5元/(吨·千米)，且这两次运输共支出铁路运费124800元，公路运费19500元．
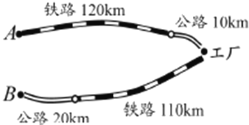
（1）设原料重x吨，产品重y吨，根据题中数量关系填写下表
原料x吨 | 产品y吨 | 合计（元） | |
铁路运费 | 124800 | ||
公路运费 | 19500 |
根据上表列方程组求原料和产品的重量．
（2）这批产品的销售款比原料费与运输费的和多多少元?
