题目内容
【题目】依次连接菱形的四边中点得到的四边形一定是( )
A. 矩形 B. 菱形 C. 正方形 D. 三角形
【答案】A
【解析】
先连接AC、BD,由于E、H是AB、AD中点,利用三角形中位线定理可知EH∥BD,同理易得FG∥BD,那么有EH∥FG,同理也有EF∥HG,易证四边形EFGH是平行四边形,而四边形ABCD是菱形,利用其性质有AC⊥BD,就有∠AOB=90°,再利用EF∥AC以及EH∥BD,两次利用平行线的性质可得∠HEF=∠BME=90°,即可得证.
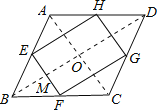
如图:连接AC、BD,相交于点O,
∵E、H是AB、AD中点,
∴EH∥BD,
同理有FG∥BD,
∴EH∥FG,且EH=FG
同理EF∥HG,
∴四边形EFGH是平行四边形,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠AOB=90°,
又∵EF∥AC,
∴∠BME=90°,
∵EH∥BD,
∴∠HEF=∠BME=90°,
∴四边形EFGH是矩形.
故选A.

练习册系列答案
相关题目
【题目】某校欲招聘一名数学教师,学校对甲、乙、丙三位候选人进行了三项能力测试,各项测试成绩满分均为100分,根据结果择优录用.三位候选人的各项测试成绩如下表所示:
测试项目 | |||
测试成绩/分 | |||
甲 | 乙 | 丙 | |
教学能力 | 85 | 73 | 73 |
科研能力 | 70 | 71 | 65 |
组织能力 | 64 | 72 | 84 |
(1)如果根据三项测试的平均成绩,谁将被录用,说明理由;
(2)根据实际需要,学校将教学、科研和组织三项能力测试得分按5∶3∶2的比例确定每人的成绩,谁将被录用,说明理由.