题目内容
【题目】已知四边形![]() 的一组对边
的一组对边![]() 的延长线相交于点
的延长线相交于点![]() .
.

(1)如图1,若![]() ,求证
,求证![]() ;
;
(2)如图2,若![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的面积为6,求四边形
的面积为6,求四边形![]() 的面积;
的面积;
(3)如图3,另一组对边![]() 的延长线相交于点
的延长线相交于点![]() ,若
,若![]() ,
,![]() ,
,![]() ,直接写出
,直接写出![]() 的长(用含
的长(用含![]() 的式子表示).
的式子表示).
【答案】(1)证明见解析;(2)75-18![]() ;(3)
;(3)![]()
【解析】
试题分析:(1)证明ΔEAB∽ΔECD,即可得解.
(2)过点C作CG⊥AD于点G,过点A作AH⊥BC于点H,在RtΔCDG中利用已知条件可求出DG、CG的长,再根据ΔCDE的面积为6,可求出ED的长,在ΔABH中可求出BH 、AH长,利用(1)可知ΔECG∽ΔEAH,从而可求出EH的长,利用S四边形ABCD=SΔAEH-SΔECG-SΔABH即可得解;
(3)由(1)(2)提供的思路即可求解.
试题解析:(1)∵∠ADC=90°
∴∠EDC=90°
∴∠ABE=∠CDE
又∵∠AEB=∠CED
∴ΔEAB∽ΔECD
∴![]()
∴![]()
(2) 过点C作CG⊥AD于点G,过点A作AH⊥BC于点H,
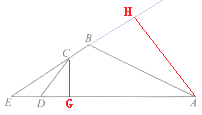
∵CD=5,cos∠ADC=![]()
∴DG=3,CG=4
∵SΔCED=6
∴ED=3
∴EG=6
∵AB=12 ∠ABC=120°
∴BH=6 AH=6![]()
由(1)有:ΔECG∽ΔEAH
∴![]()
∴EH=9![]()
∴S四边形ABCD=SΔAEH-SΔECG-SΔABH
=![]()
=75-18![]()
(3)![]()

练习册系列答案
相关题目