��Ŀ����
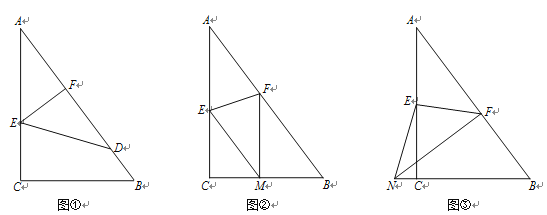
����Ŀ����ͼ����֪һ��ֱ��������ֽƬACB�����С�ACB��90�㣬AC��4��BC��3��E��F�ֱ���AC��AB���ϵ㣬����EF����ֽƬACB��һ����EF�۵���
��1����ͼ�٣����۵����A����AB���ϵĵ�D������ʹS�ı���ECBF��3S��AEF����AE�� ��
��2����ͼ�ڣ����۵����A����BC���ϵĵ�M������ʹMF��CA����AE�ij���
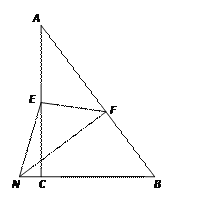
��3����ͼ�ۣ����۵����A����BC�ӳ����ϵĵ�N������ʹNF��AB����AE�ij���
���𰸡���1��AE��![]() ����2��
����2��![]() ����3��
����3��![]()
����������1��AE��![]() ��������������2��
��������������2��
��2����ͼ�ڣ���AE��x����CE��4��x��
�ߡ�ACB��90�㣬AC��4��BC��3����AB��5��
���۵���֪��AE��EM��x��AF��MF����AFE����MFE��
��MF��AC�����AEF����MFE�����AEF����AFE��
��AE��AF����AE��EM��MF��AF��
���ı���AEMFΪ���Σ�������������4��
��EM��AB�����CME�ס�CBA��������������5��
��![]() ��
��![]() ����
����![]() ��
��![]() �����x��
�����x��![]() ����AE��
����AE��![]() ������������6��
������������6��
��3����ͼ�ۣ���AE��y����CE��4��y��
���۵���֪��AE��EN��y��AF��NF��
��NF��AB�����NFB��90�㣮�ߡ�ACB��90�㣬���NFB����ACB��
 �ҡ�NBF����ABC�����NBF �ס�ABC��������������7��
�ҡ�NBF����ABC�����NBF �ס�ABC��������������7��
��![]() ��
��![]() ��
��![]() ����BF��
����BF��![]() NF��
NF��![]() AF����BF+ AF��AB��5��
AF����BF+ AF��AB��5��
��ã�BF��![]() ��NF��
��NF��![]() ��������������8��
��������������8��
��BN��![]() ��CN��BN��BC��
��CN��BN��BC��![]() ��3��
��3��![]() ��������������9��
��������������9��
![]() ��Rt��CEN����CN2+CE2��EN2����(
��Rt��CEN����CN2+CE2��EN2����(![]() )2+(4��y)2��y2��
)2+(4��y)2��y2��
��ã�y��![]() ����AE��
����AE��![]() ��
��

 ������״Ԫ���Ծ�ϵ�д�
������״Ԫ���Ծ�ϵ�д�