题目内容
【题目】如图,平面直角坐标系xOy中,点A是直线y=![]() x+
x+![]() 上一动点,将点A向右平移1个单位得到点B,点C(1,0),则
上一动点,将点A向右平移1个单位得到点B,点C(1,0),则
OB+CB的最小值为____.

【答案】![]()
【解析】∵点A是直线y=![]() x+
x+![]() 上一动点,将点A向右平移1个单位得到点B,
上一动点,将点A向右平移1个单位得到点B,
∴点B所在直线为y=![]() (x-1)+
(x-1)+![]() ,即y=
,即y=![]() x+
x+![]()
作原点关于直线y=![]() x+
x+![]() 对称点O’,连接O’C,交直线y=
对称点O’,连接O’C,交直线y=![]() x+
x+![]() 于点B,则此时有OB+CB的最小值即为O’C长度,如下图所示:
于点B,则此时有OB+CB的最小值即为O’C长度,如下图所示:
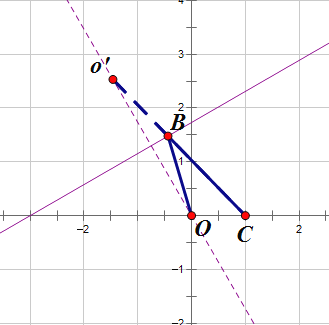
直线OO’的解析式为y=- ![]() ,则与直线直线y=
,则与直线直线y=![]() x+
x+![]() 交点坐标为(
交点坐标为(![]() ),所以点O’的坐标为(
),所以点O’的坐标为(![]() ),又因为点C(1,0),所以点C与O’的水平距离为
),又因为点C(1,0),所以点C与O’的水平距离为![]() ,垂直距离为
,垂直距离为![]() ,所以O’C的距离为:
,所以O’C的距离为: 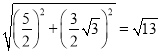 ,即为OB+CB的最小值;
,即为OB+CB的最小值;
故答案是: ![]() 。
。

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目