题目内容
1.化简(1)2a-3b+(a-b)
(2)$\frac{1}{3}$x2y-$\frac{1}{2}$xy2+$\frac{1}{2}$xy2+xy-x2y.
分析 根据合并同类项的法则即可求出答案.
解答 解:(1)原式=2a-3b+a-b=3a-4b,
(2)原式=$\frac{1}{3}$x2y-x2y-$\frac{1}{2}$xy2+$\frac{1}{2}$xy2+xy=-$\frac{2}{3}$x2y+xy
点评 本题考查合并同类项,涉及去括号法则,属于基础题型.

练习册系列答案
相关题目
16.下列计算正确的是( )
?①8-10=-2?②-8÷(-$\frac{1}{2}$)=4?③-4×(-3)=-12 ④-3-5=-8 ⑤$\frac{-8}{-16}$=2 ⑥(-22)+1=5.
?①8-10=-2?②-8÷(-$\frac{1}{2}$)=4?③-4×(-3)=-12 ④-3-5=-8 ⑤$\frac{-8}{-16}$=2 ⑥(-22)+1=5.
| A. | 2个 | B. | 6个 | C. | 4个 | D. | 5个 |
10.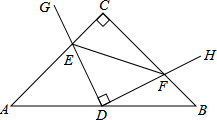 在Rt△ABC中,AC=BC,点D为AB中点.∠GDH=90°,∠GDH绕点D旋转,DG、DH分别与边AC、BC交于E,F两点.下列结论:
在Rt△ABC中,AC=BC,点D为AB中点.∠GDH=90°,∠GDH绕点D旋转,DG、DH分别与边AC、BC交于E,F两点.下列结论:
①AE+BF=$\frac{\sqrt{2}}{2}$AB,②△DEF始终为等腰直角三角形,
③S四边形CEDF=$\frac{1}{8}$AB2,
④AE2+CE2=2DF2.
其中正确的是( )
 在Rt△ABC中,AC=BC,点D为AB中点.∠GDH=90°,∠GDH绕点D旋转,DG、DH分别与边AC、BC交于E,F两点.下列结论:
在Rt△ABC中,AC=BC,点D为AB中点.∠GDH=90°,∠GDH绕点D旋转,DG、DH分别与边AC、BC交于E,F两点.下列结论:①AE+BF=$\frac{\sqrt{2}}{2}$AB,②△DEF始终为等腰直角三角形,
③S四边形CEDF=$\frac{1}{8}$AB2,
④AE2+CE2=2DF2.
其中正确的是( )
| A. | ①②③④ | B. | ①②③ | C. | ①④ | D. | ②③ |
11. 有理数a、b在数轴上的位置如图所示,则化简|a-b|+a的结果为( )
有理数a、b在数轴上的位置如图所示,则化简|a-b|+a的结果为( )
 有理数a、b在数轴上的位置如图所示,则化简|a-b|+a的结果为( )
有理数a、b在数轴上的位置如图所示,则化简|a-b|+a的结果为( )| A. | b | B. | -b | C. | -2a-b | D. | 2a-b |
 有理数a、b、c在数轴上的位置如图,|a|-|a+b|-|c-a|+|b-c|=-a.
有理数a、b、c在数轴上的位置如图,|a|-|a+b|-|c-a|+|b-c|=-a.
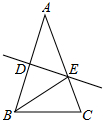 如图,在△ABC中,边AB的垂直平分线交AC于E,△ABC与△BEC的周长分别为24
如图,在△ABC中,边AB的垂直平分线交AC于E,△ABC与△BEC的周长分别为24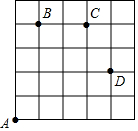 如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走均为正,向下向左走均为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向.
如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走均为正,向下向左走均为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向.