题目内容
【题目】如图,正方形![]() 的边长为
的边长为![]() ,点
,点![]() 从
从![]() 开始沿折线
开始沿折线![]() 以
以![]() 的速度移动,点
的速度移动,点![]() 从
从![]() 开始沿
开始沿![]() 边以
边以![]() 的速度移动,如果点
的速度移动,如果点![]() ,
,![]() 分别从
分别从![]() ,
,![]() 同时出发,当其中一点到达
同时出发,当其中一点到达![]() 时,另一点也随之停止运动.
时,另一点也随之停止运动.

(1)设![]() 的面积为
的面积为![]() ,
,![]() 为运动时间,写出
为运动时间,写出![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)![]() 为何值时,
为何值时,![]() 的面积为正方形
的面积为正方形![]() 面积的
面积的![]() ?
?
【答案】(1)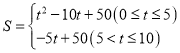 ;(2)当t=5s时,
;(2)当t=5s时,![]() 的面积为正方形
的面积为正方形![]() 面积的
面积的![]() .
.
【解析】
(1)当0≤t≤5时,点P在AD上,则△PQB的面积等于正方形的面积减去三个直角三角形的面积;当5<t≤10时,点P在CD上,△PQB面积等于![]() PQ×10;
PQ×10;
(2)结合(1)中的结论,分别列出方程求解即可.
解:(1)当0≤t≤5时,点P在AD上,
由题意得:AP=2t,DP=10-2t,DQ=t,CQ=10-t,
∵S△PQB=S正方形ABCD-S△APB-S△DPQ-S△BCQ,
∴![]() ;
;
当5<t≤10时,点P在CD上,
由题意得:PQ=t-(2t-10)=10-t,
∴![]() ,
,
综上所述: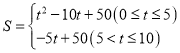 ;
;
(2)S正方形ABCD=10×10=100,
当0≤t≤5时,由题意得:![]() ,
,
解得:t=5;
当5<t≤10时,由题意得:![]() ,
,
解得:t=5(舍去),
综上,当t=5s时,![]() 的面积为正方形
的面积为正方形![]() 面积的
面积的![]() .
.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目





