题目内容
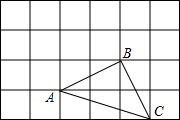
如图所示,在△ABC,∠ACB=90°,∠ABC=30°,AB=4cm,将△ABC绕点A逆时针旋转得到△AB′C′,使C′、A、B在同一直线上.
(1)求点B旋转到点B′时所经过的路线长;
(2)求在旋转过程中线段BC所扫过的面积.

(1)求点B旋转到点B′时所经过的路线长;
(2)求在旋转过程中线段BC所扫过的面积.

(1)∵∠ACB=90°,∠ABC=30°,
∴∠BAC=90°-30°=60°,
∵C′、A、B在同一直线上,
∴旋转角∠CAC′=180°-60=120°,
∴点B旋转到点B′时所经过的路线长=
=
π;
(2)∵∠ABC=30°,AB=4cm,
∴AC=
AB=
×4=2cm,
线段BC所扫过的面积=S扇形BAB′+S△AB′C′-S扇形CAC′-S△ABC,
=S扇形BAB′-S扇形CAC,
=
-
,
=4π.
∴∠BAC=90°-30°=60°,
∵C′、A、B在同一直线上,
∴旋转角∠CAC′=180°-60=120°,
∴点B旋转到点B′时所经过的路线长=
| 120•π•4 |
| 180 |
| 8 |
| 3 |
(2)∵∠ABC=30°,AB=4cm,
∴AC=
| 1 |
| 2 |
| 1 |
| 2 |
线段BC所扫过的面积=S扇形BAB′+S△AB′C′-S扇形CAC′-S△ABC,
=S扇形BAB′-S扇形CAC,
=
| 120•π•42 |
| 360 |
| 120•π•22 |
| 360 |
=4π.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目