题目内容
【题目】如图，△ABC与△A′B′C′都是等腰三角形，且AB=AC=5，A′B′=A′C′=3，若∠B+∠B′=90°，则△ABC与△A′B′C′的面积比为 ． 
【答案】25：9
【解析】解：过A作AD⊥BC于D，过A′作A′D′⊥B′C′于D′，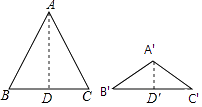 
∵△ABC与△A′B′C′都是等腰三角形，
∴∠B=∠C，∠B′=∠C′，BC=2BD，B′C′=2B′D′，
∴AD=ABsinB，A′D′=A′B′sinB′，BC=2BD=2ABcosB，B′C′=2B′D′=2A′B′cosB′，
∵∠B+∠B′=90°，
∴sinB=cosB′，sinB′=cosB，
∵S△BAC= 
ADBC= ABsinB2ABcosB=25sinBcosB，
S△A′B′C′= A′D′B′C′= A′B′cosB′2A′B′sinB′=9sinB′cosB′，
∴S△BAC：S△A′B′C′=25：9，
故答案为：25：9．
先根据等腰三角形的性质得到∠B=∠C，∠B′=∠C′，根据三角函数的定义得到AD=ABsinB，A′D′=A′B′sinB′，BC=2BD=2ABcosB，B′C′=2B′D′=2A′B′cosB′，然后根据三角形面积公式即可得到结论．
【题目】某校在践行“社会主义核心价值观”演讲比赛中，对名列前20名的选手的综合分数m进行分组统计，结果如表所示：
组号 | 分组 | 频数 |
一 | 6≤m＜7 | 2 |
二 | 7≤m＜8 | 7 |
三 | 8≤m＜9 | a |
四 | 9≤m≤10 | 2 |
（1）求a的值；
（2）若用扇形图来描述，求分数在8≤m＜9内所对应的扇形图的圆心角大小；
（3）将在第一组内的两名选手记为：A1、A2 ， 在第四组内的两名选手记为：B1、B2 ， 从第一组和第四组中随机选取2名选手进行调研座谈，求第一组至少有1名选手被选中的概率（用树状图或列表法列出所有可能结果）．
【题目】九年级（3）班数学兴趣小组经过市场调查整理出某种商品在第x天（1≤x≤90，且x为整数）的售价与销售量的相关信息如下．已知商品的进价为30元/件，设该商品的售价为y（单位：元/件），每天的销售量为p（单位：件），每天的销售利润为w（单位：元）．
时间x（天） | 1 | 30 | 60 | 90 |
每天销售量p（件） | 198 | 140 | 80 | 20 |
（1）求出w与x的函数关系式；
（2）问销售该商品第几天时，当天的销售利润最大？并求出最大利润；
（3）该商品在销售过程中，共有多少天每天的销售利润不低于5600元？请直接写出结果．
