题目内容
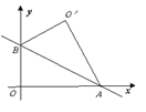
【题目】如图,直线![]() 与
与![]() 轴,
轴, ![]() 轴分别交于
轴分别交于![]() 两点,把
两点,把![]() 沿着直线
沿着直线![]() 翻折后得到
翻折后得到![]() ,则点
,则点![]() 的坐标是 ___________ 。
的坐标是 ___________ 。
【答案】(![]() ,3)
,3)
【解析】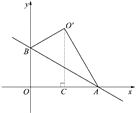
如图,过点O'作O'C⊥OA,垂足为C.
∵点A是直线与x轴的交点,
又∵当y=0时, ![]() ,
,
∴![]() ,
,
∴点A的坐标为(![]() , 0),
, 0),
∴OA=![]() .
.
∵点B是直线与y轴的交点,
又∵当x=0时, ![]() ,
,
∴点B的坐标为(0, 2),
∴OB=2.
∴在Rt△AOB中, ![]() .
.
∵在Rt△AOB中,AB=4,OB=2,即![]() ,
,
∴∠OAB=30°.
∵△AOB沿直线AB翻折得到△AO'B,
∴△AOB≌△AO'B,
∴∠O'AB=∠OAB=30°,O'A=OA=![]() .
.
∴∠OAO'=∠OAB+∠O'AB=60°,即∠CAO'=60°,
∴在Rt△O'CA中,∠AO'C=90°-∠CAO'=90°-60°=30°,
∴在Rt△O'CA中, ![]() ,
, ![]() ,
,
∴OC=OA-AC=![]() -
-![]() =
=![]() .
.
∵OC=![]() ,O'C=3,
,O'C=3,
∴点O'的坐标为(![]() , 3).
, 3).
故本题应填写:(![]() , 3).
, 3).

练习册系列答案
相关题目