题目内容
【题目】如图1，在直角坐标系xoy中，直线l与x、y轴分别交于点A（4，0）、B（0， 
）两点，∠BAO的角平分线交y轴于点D．点C为直线l上一点，以AC为直径的⊙G经过点D，且与x轴交于另一点E． 
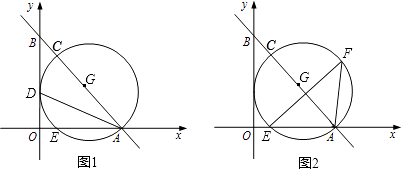
（1）求证：y轴是⊙G的切线；
（2）请求⊙G的半径r，并直接写出点C的坐标；
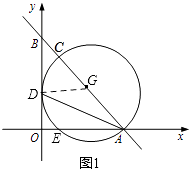
（3）如图2，若点F为⊙G上的一点，连接AF，且满足∠FEA=45°，请求出EF的长？
【答案】
（1）解：连接GD，
∵∠OAB的角平分线交y轴于点D，
∴∠GAD=∠DAO，
∵GD=GA，
∴∠GDA=∠GAD，
∴∠GDA=∠DAO，
∴GD∥OA，
∴∠BDG=∠BOA=90°，
∵GD为半径，
∴y轴是⊙G的切线；
（2）解：∵A（4，0），B（0， 
），
∴OA=4，OB= ，
在Rt△AOB中，由勾股定理可得：AB= 
，
设半径GD=r，则BG= ﹣r，
∵GD∥OA，
∴△BDG∽△BOA，
∴ 
= 
，
∴ r=4（ ﹣r），
∴r= 
；
∴C的坐标为（1，4）
（3）解：过点A作AH⊥EF于H，连接CE、CF，
∵AC是直径，
∴AC=2× =5
∴∠AEC=∠AFC=90°
∵∠FEA=45°
∴∠FCA=45°
∴在Rt△AEH中，
由勾股定理可知：AF=CF= 
，
设OE=a
∴AE=4﹣a
∵CE∥OB
∴△ACE∽△ABO
∴ 
= 
∴CE= 
∵CE2+AE2=AC2，
∴ 
（4﹣a）2+（4﹣a）2=25
∴a=1或a=7（不合题意，舍去）
∴AE=3
∴在Rt△AEH中，
由勾股定理可得，AH=EH= 
，
∴在Rt△AEH中，
由勾股定理可知：FH2=AF2﹣AH2= 
﹣ 
=8，
∴FH=2 
，
∴EF=EH+FH= 
．
【解析】（1）要证明y轴是⊙G的切线，只需要连接GD后证明GD⊥OB即可．（2）由（1）可知GD∥OA，则△BDG∽△BOA，设半径为r后，利用对应边的比相等列方程即可求出半径r的值．（3）由于∠FEA=45°，所以可以连接CE、CF构造直角三角形．由于要求的EF是弦，所以过点A作AH⊥EF，然后利用垂径定理即可求出EF的长度．
