题目内容
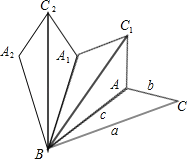
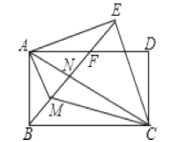
【题目】如图,以△ABC的三边为边在BC同侧分别作等边三角形,即△ABD,△BCE,△ACF.
(1)四边形ADEF为__________四边形;
(2)当△ABC满足条件____________时,四边形ADEF为矩形;
(3)当△ABC满足条件____________时,四边形ADEF为菱形;
(4)当△ABC满足条件____________时,四边形ADEF不存在.
【答案】(1)平行;(2)∠BAC=150°;(3)AB=AC且∠BAC≠60°;(4)∠BAC=60°.
【解析】
(1)可先证明△ABC≌△DBE,可得DE=AC,又有AC=AF,可得DE=AF,同理可得AD=EF,根据两组对边分别相等的四边形是平行四边形,可证四边形ADEF是平行四边形;
(2)如四边形ADEF是矩形,则∠DAF=90°,又有∠BAD=∠FAC=60°,可得∠BAC=150°,故∠BAC=150°时,四边形ADEF是矩形;
(3)利用菱形的性质与判定得出即可;
(4)根据∠BAC=60°时,∠DAF=180°,此时D、A、F三点在同一条直线上,以A,D,E,F为顶点的四边形就不存在.
(1)证明:∵△ABD,△BCE都是等边三角形,
∴∠DBE=∠ABC=60°-∠ABE,AB=BD,BC=BE.
在△ABC和△DBE中
 ,
,
∴△ABC≌△DBE(SAS).
∴DE=AC.
又∵AC=AF,
∴DE=AF.
同理可得EF=AD.
∴四边形ADEF是平行四边形.
(2)∵四边形ADEF是平行四边形,
∴当∠DAF=90°时,四边形ADEF是矩形,
∴∠FAD=90°.
∴∠BAC=360°-∠DAF-∠DAB-∠FAC=360°-90°-60°-60°=150°.
则当∠BAC=150°时,四边形ADEF是矩形;
故答案为:∠BAC=150°;
(3)当AB=AC且∠BAC≠60°时,四边形ADEF是菱形,
理由是:由(1)知:AD=AB=EF,AC=DE=AF,
∵AC=AB,
∴AD=AF,
∵四边形ADEF是平行四边形,AD=AF,
∴平行四边形ADEF是菱形.
故答案为:AB=AC且∠BAC≠60°(或AB=AC≠BC);
(4)当∠BAC=60°时,∠DAF=180°,
此时D、A、F三点在同一条直线上,以A,D,E,F为顶点的四边形就不存在;
故答案为:∠BAC=60°.

【题目】某水果批发商欲将A市的一批水果运往B市销售,有火车和汽车两种运输工具,运输过程中的损耗均为160元/时。有关数据如下:
运输工具 | 平均速度(千米/时) | 运费(元/千米) | 装卸费(元) |
火车 | 100 | 18 | 1800 |
汽车 | 80 | 22 | 1000 |
(1)如果汽车的总支出费用比火车费用多960元,求出A市与B市之间的路程是多少千米?请列方程解答。
(2)如果A市与C市之间的距离为300千米,要想将这批水果运往C市销售。选择哪种运输工具比较合算呢?请通过计算说明你的理由。