题目内容
【题目】（探索新知）
如图1，点C在线段AB上，图中共有3条线段：AB、AC和BC，若其中有一条线段的长度是另一条线段长度的两倍，则称点C是线段AB的“二倍点”．
（1）一条线段的中点 这条线段的“二倍点”；（填“是”或“不是”）
（深入研究）
如图2，若线段AB＝20cm，点M从点B的位置开始，以每秒2cm的速度向点A运动，当点M到达点A时停止运动，运动的时间为t秒．
（2）问t为何值时，点M是线段AB的“二倍点”；
（3）同时点N从点A的位置开始，以每秒1cm的速度向点B运动，并与点M同时停止．请直接写出点M是线段AN的“二倍点”时t的值．
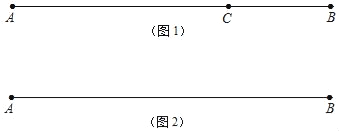
【答案】（1）是；（2）t为
或5或
时；（3）t为7.5或8或
时
【解析】
(1)可直接根据“二倍点”的定义进行判断即可；
(2)用含t的代数式分别表示出线段AM、BM、AB，然后根据“二倍点”的意义，分类讨论即可得结果；
(3)用含t的代数式分别表示出线段AN、NM、AM，然后根据“二倍点”的意义，分类讨论即可．
(1)因为线段的中点把该线段分成相等的两部分，
该线段等于2倍的中点一侧的线段长，
所以一条线段的中点是这条线段的“二倍点”，
故答案为：是；
(2)当AM＝2BM时，20﹣2t＝2×2t，解得：t＝；
当AB＝2AM时，20＝2×(20﹣2t)，解得：t＝5；
当BM＝2AM时，2t＝2×(20﹣2t)，解得：t＝；
答：t为或5或时，点M是线段AB的“二倍点”；
(3)当AN＝2MN时，t＝2[t﹣(20﹣2t)]，解得：t＝8；
当AM＝2NM时，20﹣2t＝2[t﹣(20﹣2t)]，解得：t＝7.5；
当MN＝2AM时，t﹣(20﹣2t)＝2(20﹣2t)，解得：t＝；
答：t为7.5或8或时，点M是线段AN的“二倍点”．
练习册系列答案
相关题目
