题目内容
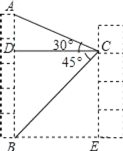
【题目】小宇在学习解直角三角形的知识后,萌生了测量他家对面位于同一水平面的楼房高度的想法,他站在自家C处测得对面楼房底端B的俯角为45°,测得对面楼房顶端A的仰角为30°,并量得两栋楼房间的距离为9米,请你用小宇测得的数据求出对面楼房AB的高度.(结果保留到整数,参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7)
≈1.7)
【答案】楼房AB的高度约为14米.
【解析】
利用直角三角形特殊函数值进行求解即可,在Rt△ADC中,tan∠ACD=![]() ,继而求出AD,在Rt△ADB中,tan∠BCD=
,继而求出AD,在Rt△ADB中,tan∠BCD=![]() ,继而求出BD=CD=9,继而即可求解.
,继而求出BD=CD=9,继而即可求解.
解:在Rt△ADC中,tan∠ACD=![]() ,
,
∴AD=DCtan∠ACD=9×![]() =
=![]() 米,
米,
在Rt△ADB中,tan∠BCD=![]() ,
,
∴BD=CD=9米,
∴AB=AD+BD=![]() +9≈14米.
+9≈14米.
答:楼房AB的高度约为14米.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
【题目】阅读对学生的成长有着深远的影响.某中学为了解学生每周课余阅读的时间,在本校随机抽取若干名学生进行调查,并依据调查结果经制了以下不完整的统计图表.
组别 | 时间(小时) | 频数(人数) | 频率 |
A |
| 6 |
|
B |
|
|
|
C |
| 10 |
|
D |
| 8 |
|
E |
| 4 |
|
合计 | 1 |
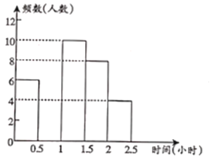
请根据图表中的信息,解答下列问题:
(1)表中的![]() ,
,![]() ,将频数分布直方图补全;
,将频数分布直方图补全;
(2)估计该校2000名学生中,每周课余阅读时间不足1小时的学生大约有多少名?
(3)![]() 组的4人中,有1名男生和3名女生,该校计划在
组的4人中,有1名男生和3名女生,该校计划在![]() 组学生中随机选出两人向全校同学作读书心得报告,求抽取的两名学生刚好是1名男生和1名女生的概率.
组学生中随机选出两人向全校同学作读书心得报告,求抽取的两名学生刚好是1名男生和1名女生的概率.