题目内容
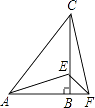
【题目】如图,在△ABC中,AD⊥BC且BD>CD,DF⊥AB,△CDE和△ADB都是等腰直角三角形,给出下列结论,正确的是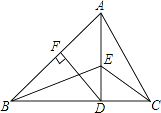
①△ADC≌△BDE;
②△ADF≌△BDF;
③△CDE≌△AFD;
④△ACE≌ABE.
【答案】①②
【解析】解:①∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∵△CDE和△ADB都是等腰直角三角形,
∴ED=DC,AD=BD,
在△ADC和△BDE中,
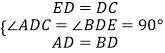 ,
,
∴△ADC≌△BDE(SAS),故本选项正确;
②∵DF⊥AB,
∴∠AFD=∠BFD=90°,
在RT△ADF和RT△BDF中,
![]() ,
,
∴△ADF≌△BDF(HL),故本选项正确;
③易证得△AFD是等腰直角三角形,
因为无法证得对应边相等,故无法证明△CDE≌△AFD,故本选项错误;
④∵AD=AD,BD>BC,根据勾股定理可得:AC≠AB,即△ACE和△ABE不全等,故本选项错误;
所以答案是①②.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目