题目内容
【题目】如图,在△ABC中,AB=BC,∠ABC=90°,点F为AB延长线上一点,点E在BC上,BE=BF,连接AE,EF和CF.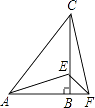
(1)求证:△ABE≌△CBF;
(2)若∠CAE=30°,求∠EFC的度数.
【答案】
(1)证明:∵∠ABC=90°,F为AB延长线上一点,
∴∠ABC=∠CBF=90°.
在△ABE和△CBF中,
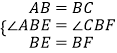 ,
,
∴△ABE≌△CBF
(2)解:∵在△ABC中,AB=BC,∠ABC=90°,点F为AB延长线上一点,点E在BC上,BE=BF,
∴△ABC和△EBF都是等腰直角三角形,
∴∠ACB=∠EFB=45°.
∵∠CAE=30°,
∴∠AEB=∠CAE+∠ACB=30°+45°=75°.
由(1)知△ABE≌△CBF,
∴∠CFB=∠AEB=75°.
∴∠EFC=∠CFB﹣∠EFB=75°﹣45°=30°
【解析】(1)根据已知条件由SAS得到△ABE≌△CBF;(2)由已知可得△ABC和△EBF都是等腰直角三角形,再根据由(1)知△ABE≌△CBF,求出∠EFC的度数.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目