Question

【题目】定义：若抛物线的顶点和与x轴的两个交点所组成的三角形为等边三角形时．则称此抛物线为正抛物线．

概念理解：

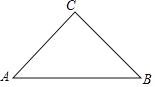
（1）如图，在△ABC中，∠BAC＝90°，点D是BC的中点．试证明：以点A为顶点，且与x轴交于D、C两点的抛物线是正抛物线；

问题探究：

（2）已知一条抛物线经过x轴的两点E、F（E在F的左边），E（1，0）且EF＝2若此条抛物线为正抛物线，求这条抛物线的解析式；

应用拓展：

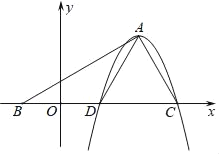
（3）将抛物线y1＝﹣x2+2x+9向下平移9个单位后得新的抛物线y2．抛物线y2的顶点为P，与x轴的两个交点分别为M、N（M在N左侧），把△PMN沿x轴正半轴无滑动翻滚，当边PN与x轴重合时记为第1次翻滚，当边PM与x轴重合时记为第2次翻滚，依此类推…，请求出当第2019次翻滚后抛物线y2的顶点P的对应点坐标．

Answer 1

【答案】（1）详见解析；（2）y＝或y＝；（3）当第2019次翻滚后抛物线y2的顶点P的对应点坐标为（4039，3）．

【解析】

（1）由Rt△ABC中AD是斜边BC的中线可得AD＝CD，由抛物线对称性可得AD＝AC，即证得△ACD是等边三角形．

（2）设抛物线顶点为G，根据正抛物线定义得△EFG是等边三角形，又易求E、F坐标，即能求G点坐标．由于不确定点G纵坐标的正负号，故需分类讨论，再利用顶点式求抛物线解析式．

（3）根据题意求出抛物线y2的解析式，并按题意求出P、M、N的坐标，得到等边△PMN，所以当△PMN翻滚时，每3次为一个周期，点P回到x轴上方，且横坐标每多一个周期即加6，其规律为当翻滚次数n能被3整除时，横坐标为： +n×2＝（2n+1）．2019能被3整除，代入即能求此时点P坐标．

解：（1）证明：∠BAC＝90°，点D是BC的中点

∴AD＝BD＝CD＝BC

∵抛物线以A为顶点与x轴交于D、C两点

∴AD＝AC

∴AD＝AC＝CD

∴△ACD是等边三角形

∴以A为顶点与x轴交于D、C两点的抛物线是正抛物线．

（2）∵E（1，0）且EF＝2，点F在x轴上且E在F的左边

∴F（3，0）

∵一条经过x轴的两点E、F的抛物线为正抛物线，设顶点为G

∴△EFG是等边三角形

∴xG＝

①当G（2，）时，设抛物线解析式为y＝a（x﹣2）2+

把点E（1，0）代入得：a+＝0

∴a＝﹣

∴y＝﹣（x﹣2）2+

②当G（2，﹣）时，设抛物线解析式为y＝a（x﹣2）2﹣

把点E（1，0）代入得：a﹣＝0

∴a＝

∴y＝（x﹣2）2﹣

综上所述，这条抛物线的解析式为y＝﹣（x﹣2）2+或y＝（x﹣2）2﹣

（3）∵抛物线y1＝﹣x2+2x+9＝﹣（x﹣）2+12

∴y1向下平移9个单位后得抛物线y2＝﹣（x﹣）2+3

∴P（，3），M（0，0），N（2，0）

∴PM＝MN＝PN＝2

∴△PMN是等边三角形

∴第一次翻滚顶点P的坐标变为P1（4，0），第二次翻滚得P2与P1相同，第三次翻滚得P3（7，3）

即每翻滚3次为一个周期，当翻滚次数n能被3整除时，点P纵坐标为3，横坐标为： +n×2＝（2n+1）

∵2019÷3＝673

∴（2×2019+1）×＝4039

∴当第2019次翻滚后抛物线y2的顶点P的对应点坐标为（4039，3）．