题目内容
【题目】在平面直角坐标系中,点![]() 的坐标满足:
的坐标满足:![]()
(1)求出点![]() 的坐标
的坐标
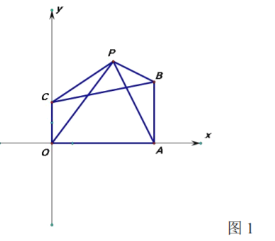
(2)如图1,连接![]() ,点
,点![]() 在四边形
在四边形![]() 外面且在第一象限,再连
外面且在第一象限,再连![]() ,则
,则![]() ,求
,求![]() 点坐标.
点坐标.
(3)如图2所示,![]() 为线段
为线段![]() 上一动点,
上一动点,![]() (在
(在![]() 右侧)为
右侧)为![]() 上一动点,使
上一动点,使![]() 轴始终平分
轴始终平分![]() ,连
,连![]() 且
且![]() ,那么
,那么![]() 是否为定值?若为定值,请直接写出定值,若不是,请简单说明理由.
是否为定值?若为定值,请直接写出定值,若不是,请简单说明理由.

【答案】(1)A(5,0),C(0,2);(2)P(3, ![]() );(3)
);(3)![]() 是定值,∠F=2
是定值,∠F=2![]() -180°.
-180°.
【解析】
(1)根据绝对值和平方具有非负性得到2a-5c=0,c-2=0,解之即可得到a,c的值,从而得到A,C坐标;
(2)过P作PM⊥y轴,PN⊥AB的延长线,PH⊥x轴,因为![]() ,所以可得2PM=3PN,由图知PM+PN=5,可得PM=3,PN=2,由
,所以可得2PM=3PN,由图知PM+PN=5,可得PM=3,PN=2,由![]() 得
得![]() ,即
,即![]() ,可求出PH的值,从而得到P点坐标;
,可求出PH的值,从而得到P点坐标;
(3)设∠CDF=![]() ,OE与DF的交点为M,由四边形内角和为360°,可得∠OMD的度数,根据三角形内角和为180°可得∠DEO的度数,根据已知可得∠DEF,而∠F=180°-∠DEF-∠FDE,将值代入即可求出∠F的度数.
,OE与DF的交点为M,由四边形内角和为360°,可得∠OMD的度数,根据三角形内角和为180°可得∠DEO的度数,根据已知可得∠DEF,而∠F=180°-∠DEF-∠FDE,将值代入即可求出∠F的度数.
解:(1)∵![]()
∴![]()
解得![]()
∴A(5,0),C(0,2)
(2)过P作PM⊥y轴,PN⊥AB的延长线,PH⊥x轴

由(1)知A(5,0),C(0,2),B(5,3)
∵![]()
∴![]() CO
CO![]() PM=
PM=![]() AB
AB![]() PN
PN
∴![]() ×2PM=
×2PM=![]() ×3PN
×3PN
∴2PM=3PN
∵PM+PN=5
∴PM=3,PN=2
∵![]()
∴![]()
∴![]()
∴![]()
即![]()
∴PH=![]()
∴P(3, ![]() )
)
(3)![]() 是定值,∠F=2
是定值,∠F=2![]() -180°.
-180°.
设∠CDF=![]()
∴∠FDE=180°-2![]()
设OE与DF的交点为M

∴∠OMD=360°-![]() -
-![]() -90°=270°-
-90°=270°-![]() -
-![]()
∴∠DEO=∠OMD-∠FDE=90°+![]() -
-![]()
∴∠DEF=2∠DEO=180°+2![]() -2
-2![]()
∴∠F=180°-∠DEF-∠FDE=2![]() -180°
-180°
故答案为(1)A(5,0),C(0,2);(2)P(3, ![]() );(3)
);(3)![]() 是定值,∠F=2
是定值,∠F=2![]() -180°.
-180°.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案



