题目内容
【题目】在△ABC中,AB=4 ![]() ,BC=6,∠B=45°,D为BC边上一动点,将△ABC沿着过点D的直线折叠使点C落在AB边上,则CD的取值范围是 .
,BC=6,∠B=45°,D为BC边上一动点,将△ABC沿着过点D的直线折叠使点C落在AB边上,则CD的取值范围是 .
【答案】![]()
【解析】解:∵D为BC边上一动点,将△ABC沿着过点D的直线折叠使点C落在AB边上,根据轴对称的性质,则点C与点C'应在以点D为圆心,DC为半径的圆上,
∴CD的最小值的情形,是⊙D与AB相切时,CD的最大值的情形,是点C'与点A重合时.
①当⊙D与AB相切时,如图1: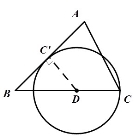
图1
过点D作DC'![]() AB于点C',设CD=x,则DC'=CD=x,
AB于点C',设CD=x,则DC'=CD=x,
∵∠B=45°,∴BD=![]() x,
x,
∴![]() x+x=6,
x+x=6,
解得:x=![]() .
.
②当点C'与点A重合时,如图2: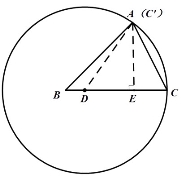
连接DA,过点A作AE![]() BC于点E,设DC=DA=x,
BC于点E,设DC=DA=x,
∵∠B=45°,∴AE=BE=4,∴EC=6-BE=6-4=2,
∴DE=x-2,
在Rt![]() ADE 中,根据勾股定理得:
ADE 中,根据勾股定理得:
x2=(x-2)2+42 ,
解得:x=5.
综合①②,可知![]() .
.
故答案是:![]() .
.
【考点精析】关于本题考查的勾股定理的概念和轴对称的性质,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;关于某条直线对称的两个图形是全等形;如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线;两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上才能得出正确答案.

练习册系列答案
相关题目