Question

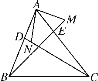
【题目】如图，△ABC中，CD、BE是边AB和AC上的高，点M在BE的延长线上，且BM＝AC，点N在CD上，且AB＝CN，则∠MAN的度数是________．

Answer 1

【答案】90°

【解析】

只要证明△ABM≌△NCA，可得∠BAM=∠CNA，由∠CNA=∠ADC+∠BAN=90°+∠BAN，∠BAM=∠MAN+∠BAN，即可推出∠MAN=90°．

∵CD、BE是边AB和AC上的高，

∴∠ADC=∠AEB=90°，

∴∠ABM+∠BAC=90°,∠BAC+∠ACN=90°，

∴∠ABM=∠ACN，

在△ABM和△ACN中，

∵AB=CN，∠ABM=∠CAN，BM=AC，

∴△ABM≌△NCA，

∴∠BAM=∠CNA，

∵∠CNA=∠ADC+∠BAN=90°+∠BAN，∠BAM=∠MAN+∠BAN，

∴∠MAN=90°.

故答案为90°.