Question

【题目】实践操作

如图1，在矩形纸片ABCD中，AB＞AD.

第一步：如图2，将图1中的矩形纸片ABCD沿过点A的直线折叠，使点D落在AB上的点E处，折痕为AF，再沿EF折叠，然后把纸片展平．

第二步：如图3，将图2中的矩形纸片再次折叠，使点D与点F重合，折痕为GH，然后展平，隐去AF．

第三步：如图4，将图3中的矩形纸片沿AH折叠，得到△AD′H，再沿AD′折叠，折痕为AM，AM与折痕EF交于点N，然后展平．

问题解决

(1) 如图2，说明四边形AEFD是正方形；

(2) 如图4，判断NF与ND′的数量关系，并说明理由；

探索发现

（3）图4中MH与AM之间满足MH=nAM，请求出n的值.

Answer 1

【答案】(1)见解析； (2)相等；(3).

【解析】分析:（1）先判断四边形AEFD是矩形，再由一组邻边相等可证明四边形AEFD是正方形；

（2）连接HN，由折叠的性质得DH=HF=H D′，由“HL”证明△HN D′≌△HNF即可得到NF=ND′；

（3）由面积法，即S△AMH=，即可求得n的值.

详解:（1）∵∠D=∠DAE=∠AEF,

∴四边形AEFD是矩形，

∵AD=AE,

∴四边形AEFD是正方形；

（2）∵DH=HF，DH=H D′，

∴HF=H D′.

又∵HN=HN,

∴△HN D′≌△HNF（HL），

∴NF=ND′；

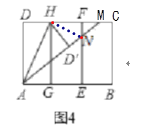
（3）∵,

AD=2DH=2 H D′,

∴AM=2HM,

∴HM=AM,

∵MH=nAM，

∴n=.