Question

【题目】阅读材料：

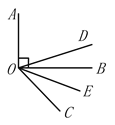
如图1，点是直线上一点，上方的四边形中，，延长，，探究与的数量关系，并证明.

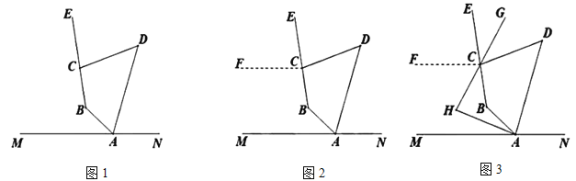
小白的想法是：“作（如图2），通过推理可以得到，从而得出结论”.

请按照小白的想法完成解答：

拓展延伸：

保留原题条件不变，平分，反向延长，交的平分线于点（如图3），设，请直接写出的度数（用含的式子表示）.

Answer 1

【答案】阅读材料：，见解析；拓展延伸：.

【解析】

（1）作，，，由平行线性质可得，结合已知，可证，进而得到，从而，，将代入可得.

（2）过H点作HP∥MN，可得∠CHA=∠PHA+∠PHC，结合（1）的结论和CG平分∠ECD可得∠PHC =∠FCH =120°-，即可得.

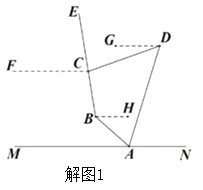
解：【阅读材料】

作，，（如图1）.

∵，

∴.

∴.

∵，

∴.

∴

∴.

∵，

∴.

∵，

∴.

∴，.

∴.

∵，

∴.

【拓展延伸】

结论：.

理由：如图，作，过H点作HP∥MN，

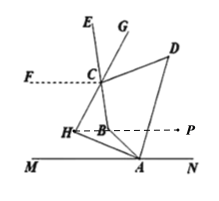
∴∠PHA=∠MAH=，

由（1）得FC∥MN，

∴FC∥HP，

∴∠PHC=∠FCH，

∵,CG平分∠ECD，

∴∠ECG=20°+，

∴∠FCH=

=180°-()-(20°+)

=120°-

∴∠CHA=∠PHA+∠PHC=+（120°-）=120°-

即：.