题目内容
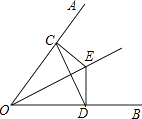
【题目】如图,⊙O中,直径CD⊥弦AB于E,AM⊥BC于M,交CD于N,连接AD.
(1)求证:AD=AN;
(2)若AB=8,ON=1,求⊙O的半径.

【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)先根据圆周角定理得出∠BAD=∠BCD,再由直角三角形的性质得出∠ANE=∠CNM,故可得出∠BCD=∠BAM,由全等三角形的判定定理得出△ANE≌△ADE,故可得出结论;
(2)先根据垂径定理求出AE的长,设NE=x,则OE=x-1,NE=ED=x,r=OD=OE+ED=2x-1
连结AO,则AO=OD=2x-1,在Rt△AOE中根据勾股定理可得出x的值,进而得出结论.
试题解析:
(1)证明:∵CD⊥AB
∴∠CEB=90
∴∠C+∠B=90.
同理∠C+∠CNM=90
∴∠CNM=∠B.
∵∠CNM=∠AND
∴∠AND=∠B
∵弧AC=弧AC
∴∠D=∠B
∴∠AND=∠D
∴AN=AD
(2)解:设ON的长为![]() ,连接OA
,连接OA
∵AN=AD,CD⊥AB
∴DE=NE= ![]()
∴OD=OE+ED= ![]()
∴OA=OD![]() .
.
∴在Rt△OAE中![]()
∴![]()
解得![]() 或
或![]() (不合题意,舍去).
(不合题意,舍去).
∴OA![]() .
.
即⊙O的半径为![]() .
.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
【题目】某灯具厂计划一天生产300盏景观灯,但由于各种原因,实际每天生产景观灯数与计划每天生产景观灯数相比有出入.下表是某周的生产情况(增产记为正、减产记为负):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 |
|
|
|
|
|
|
|
(1)求该厂本周实际生产景观灯的盏数;
(2)求产量最多的一天比产量最少的一天多生产景观灯的盏数;
(3)该厂实行每日计件工资制,每生产一盏景观灯可得60元,若超额完成任务,则超过部分每盏另奖20元,若未能完成任务,则少生产一盏扣25元,那么该厂工人这一周的工资总额是多少元?