Question

【题目】如图，已知E是∠AOB的平分线上的一点，EC⊥OA，ED⊥OB，垂足分别是C，D．求证：OE垂直平分CD．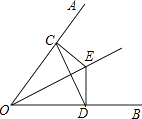

Answer 1

【答案】证明：∵E是∠AOB的平分线上一点，EC⊥OA，ED⊥OB，
∴DE=CE，OE=OE，
在Rt△ODE与Rt△OCE中，
，
∴Rt△ODE≌Rt△OCE（HL），
∴OD=OC，
∴△DOC是等腰三角形，
∵OE是∠AOB的平分线，
∴OE是CD的垂直平分线
【解析】先根据E是∠AOB的平分线上一点，EC⊥OB，ED⊥OA得出△ODE≌△OCE，可得出OD=OC，DE=CE，OE=OE，可得出△DOC是等腰三角形，由等腰三角形的性质即可得出OE是CD的垂直平分线．
【考点精析】掌握角平分线的性质定理和线段垂直平分线的性质是解答本题的根本，需要知道定理1：在角的平分线上的点到这个角的两边的距离相等； 定理2：一个角的两边的距离相等的点，在这个角的平分线上；垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线；线段垂直平分线的性质定理：线段垂直平分线上的点和这条线段两个端点的距离相等．