题目内容
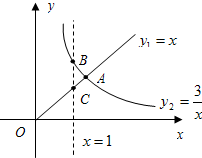函数y1=x(x≥0)，y2=| 3 |
| x |
（1）两函数图象的交点A的坐标为（
| 3 |
| 3 |
（2）当x=1时，BC=2；
（3）当x＞
| 3 |
（4）当x逐渐增大时，y1随着x的增大而增大，y2随着x的增大而减小．
其中正确结论的序号是（ ）
分析：将正比例函数与反比例函数解析式联立，消去y后求出x的值，确定出A的坐标，即可对（1）做出判断；
将x=1分别代入正比例与反比例解析式，求出对应的纵坐标的值，相减后即可求出BC的长，即可对（2）做出判断；
由图象可知，当x＞
时，y1的图象在y2图象上方，即x＞
时，y1＞y2，故（3）错误；
由在第一象限正比例函数为增函数，反比例函数为减函数，即可对（4）做出判断．
将x=1分别代入正比例与反比例解析式，求出对应的纵坐标的值，相减后即可求出BC的长，即可对（2）做出判断；
由图象可知，当x＞
| 3 |
| 3 |
由在第一象限正比例函数为增函数，反比例函数为减函数，即可对（4）做出判断．
解答：解：联立两函数解析式得：
，
解得：
，
∴A（
，
），故（1）正确；
将x=1代入一次函数得：y1=1；将x=1代入反比例函数得：y2=
=3，
则BC=3-1=2，故（2）正确；
由函数图象可得：当x＞
时，y1＞y2，故（3）错误；
在第一象限，正比例函数y1=x为增函数，即y随x的增大而增大；
在第一象限，反比例函数
为减函数，即y随x的增大而减小，
故（4）正确．
综上，正确的选项有（1）（2）（4）．
故选B
|
解得：
|
∴A（
| 3 |
| 3 |
将x=1代入一次函数得：y1=1；将x=1代入反比例函数得：y2=
| 3 |
| 1 |
则BC=3-1=2，故（2）正确；
由函数图象可得：当x＞
| 3 |
在第一象限，正比例函数y1=x为增函数，即y随x的增大而增大；
在第一象限，反比例函数
| 3 |
| x |
故（4）正确．
综上，正确的选项有（1）（2）（4）．
故选B
点评：此题考查了一次函数与反比例函数的交点问题，涉及的知识有：坐标与图形性质，正比例、反比例函数的图象与性质，利用了数形结合的思想，数形结合思想是数学中重要的思想方法，学生做题时注意灵活运用．
练习册系列答案
相关题目
设max{a，b}表示a、b中较大的数，如max{2，3}=3．
已知函数y1=x-1和
已知反比例函数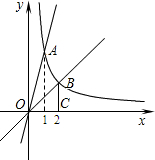
点的横坐标分别为1和2．过点B作BC垂直x轴于点C，△OBC的面积为2．