题目内容
【题目】如图,△ABC中,D点在BC上,现有下列四个命题:
①若AB=AC,则∠B=∠C;
②若AB=AC,∠1=∠2,则AD⊥BC,BD=DC;
③若AB=AC,BD=CD,则AD⊥BC,∠1=∠2;
④若AB=AC,AD⊥BC,则BD=BC,∠1=∠2.
其中正确的有( )
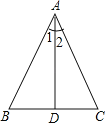
A.1个 B.2个 C.3个 D.4个
【答案】D
【解析】
试题分析:根据等腰三角形的性质对①进行判断;根据等腰三角形的“三线合一”对②③④进行判断.
解:①若AB=AC,则∠B=∠C,所以①正确;
②若AB=AC,∠1=∠2,即AD为顶角的平分线,则AD⊥BC,BD=DC,所以②正确;
③若AB=AC,BD=DC,即AD为底边上的中线,则AD⊥BC,∠1=∠2,所以③正确;
④若AB=AC,AD⊥BC,即AD为底边上的高,则BD=DC,∠1=∠2,所以④正确.
故选D.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目