Question

【题目】如图，在△ABC中，AB＝AC，点D，E，F分别在边BC，AC，AB上，且BD＝CE，DC＝BF，连结DE，EF，DF，∠1＝60°

（1）求证：△BDF≌△CED．

（2）判断△ABC的形状，并说明理由．

Answer 1

【答案】（1）见解析；（2）△ABC是等边三角形，理由见解析

【解析】

（1）用SAS定理证明三角形全等；（2）由△BDF≌△CED得到∠BFD＝∠CDE，然后利用三角形外角的性质求得∠B＝∠1＝60°，从而判定△ABC的形状.

解：（1）证明：∵AB＝AC，

∴∠B＝∠C，

在△BDF和△CED中，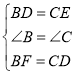

∴△BDF≌△CED（SAS）；

（2）△ABC是等边三角形，理由如下：

由（1）得：△BDF≌△CED，

∴∠BFD＝∠CDE，

∵∠CDF＝∠B+∠BFD＝∠1+∠CDE，

∴∠B＝∠1＝60°，

∵AB＝AC，

∴△ABC是等边三角形；