题目内容
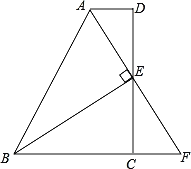
【题目】如图,AB=AC,点D,E分别在AB,AC上,补充下列一个条件后,不能判断△ABE ≌△ACD的是

A.∠B=∠CB.AD=AEC.∠BDC=∠CEBD.BE=CD
【答案】D
【解析】
欲使△ABE≌△ACD,已知AB=AC和∠A为公共角,根据各选项所添加条件,利用全等三角形判定定理AAS、SAS、ASA,逐一判断即可.
解:∵AB=AC,∠A为公共角,
A、如添∠B=∠C,利用ASA即可证明△ABE≌△ACD;
B、如添加AD=AE,利用SAS即可证明△ABE≌△ACD;
C、如添∠BDC=∠CEB,可证明∠ADC=∠AEB,利用AAS即可证明△ABE≌△ACD;
D、如添BE=CD,因为SSA不能证明△ABE≌△ACD,所以此选项不能作为添加的条件;
故选:D.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
【题目】某航空公司经营A、B、C、D四个城市之间的客运业务.若机票价格y(元)是两城市间的距离x(千米)的一次函数.今年“五一”期间部分机票价格如下表所示:
起点 | 终点 | 距离x(千米) | 价格y(元) |
A | B | 1000 | 2050 |
A | C | 800 | 1650 |
A | D | 2550 | |
B | C | 600 | |
C | D | 950 |
(1)求该公司机票价格y(元)与距离x(千米)的函数关系式;
(2)利用(1)中的关系式将表格填完整;
(3)判断A、B、C、D这四个城市中,哪三个城市在同一条直线上?请说明理由;
(4)若航空公司准备从旅游旺季的7月开始增开从B市直接飞到D市的旅游专线,且按以上规律给机票定价,那么机票定价应是多少元?