题目内容
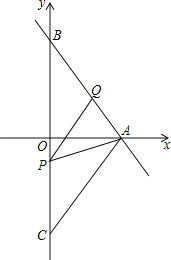
【题目】如图,己知函数y=﹣![]() x+4的图象与坐标轴的交点分别为点A、B,点C与点B关于x轴对称,动点P、Q分别在线段BC、AB上(点P不与点B、C重合).且∠APQ=∠ABO
x+4的图象与坐标轴的交点分别为点A、B,点C与点B关于x轴对称,动点P、Q分别在线段BC、AB上(点P不与点B、C重合).且∠APQ=∠ABO
(1)点A的坐标为 ,AC的长为 ;
(2)判断∠BPQ与∠CAP的大小关系,并说明理由;
(3)当△APQ为等腰三角形时,求点P的坐标.
【答案】(1)(3,0),5;(2)见解析;(3)P点坐标为(0,﹣1),(0,![]() ).
).
【解析】
试题分析:(1)利用坐标轴上点的坐标特征可求出A、B点的坐标,再利用关于x轴对称的点的坐标特征得到C点坐标,然后利用勾股定理可计算出AC的长;
(2)利用对称性质得到AB=AC,则∠1=∠2,而∠APQ=∠1,所以∠2=∠APQ,再根据三角形外角性质得∠BPA=∠2+∠3,易得∠BPQ=∠3;
(3)分类讨论:当PA=PQ,如图1,根据等腰三角形的性质得∠PQA=∠PAQ,利用三角形外角性质和等量代换可得∠PQA=∠BPA,则BP=BA=5,所以OP=BP﹣OB=1,于是得到此时P点坐标为(0,﹣1);当AQ=AP,由于∠AQP=∠APQ,∠AQP=∠BPA,两者相矛盾,此情况不存在;当QA=QP,如图2,则∠APQ=∠PAQ,由于∠1=∠APQ,则∠1=∠PAQ,所以PA=PB,设P(0,t),则PB=PA=4﹣t,在Rt△OPA中利用勾股定理得到t2+32=(4﹣t)2,解得t=![]() ,从而可得到此时P点坐标为(0,
,从而可得到此时P点坐标为(0,![]() ).
).
解:(1)当y=0时,﹣![]() x+4=0,解得x=3,则A(3,0),
x+4=0,解得x=3,则A(3,0),
当x=0时,y=﹣![]() x+4=4,则B(0,4),
x+4=4,则B(0,4),
∵点C与点B关于x轴对称,
∴C(0,﹣4),
∴AC=![]() =5;
=5;
故答案为(3,0),5;
(2)∠BPQ=∠CAP.理由如下:
∵点C与点B关于x轴对称,
∴AB=AC,
∴∠1=∠2,
∵∠APQ=∠1,
∴∠2=∠APQ,
∵∠BPA=∠2+∠3,
即∠BPQ+∠APQ=∠2+∠3,
∴∠BPQ=∠3;
(3)当PA=PQ,如图1,则∠PQA=∠PAQ,
∵∠PQA=∠1+∠BPQ=∠APQ+∠BPQ=∠BPA,
∴BP=BA=5,
∴OP=BP﹣OB=1,
∴P(0,﹣1);
当AQ=AP,则∠AQP=∠APQ,
而∠AQP=∠BPA,所以此情况不存在;
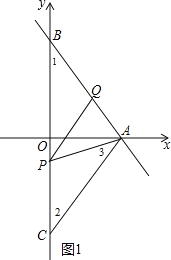
当QA=QP,如图2,则∠APQ=∠PAQ,
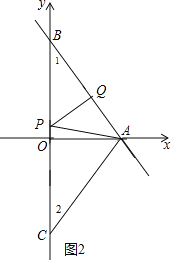
而∠1=∠APQ,
∴∠1=∠PAQ,
∴PA=PB,
设P(0,t),则PB=4﹣t,
∴PA=4﹣t,
在Rt△OPA中,∵OP2+OA2=PA2,
∴t2+32=(4﹣t)2,解得t=![]() ,
,
∴P(0,![]() ),
),
综上所述,满足条件的P点坐标为(0,﹣1),(0,![]() ).
).

 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案【题目】宿州市高新区某电子电路板厂到安徽大学从2018年应届毕业生中招聘公司职员,对应聘者的专业知识、英语水平、参加社会实践与社团活动等三项进行测试或成果认定,三项的得分满分都为100分,三项的分数分别按5∶3∶2的比例记入每人的最后总分,有4位应聘者的得分如下表所示.
| 专业知识 | 英语水平 | 参加社会实践与 社团活动等 |
甲 | 85 | 85 | 90 |
乙 | 85 | 85 | 70 |
丙 | 80 | 90 | 70 |
丁 | 90 | 90 | 50 |
(1)分别算出4位应聘者的总分;
(2)表中四人“专业知识”的平均分为85分,方差为12.5,四人“英语水平”的平均分为87.5分,方差为6.25,请你求出四人“参加社会实践与社团活动等”的平均分及方差;
(3)分析(1)和(2)中的有关数据,你对大学生应聘者有何建议?