题目内容
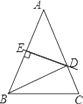
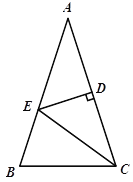
【题目】如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连结EC.
(1)求∠ECD的度数;
(2)若CE=12,求BC长.
【答案】(1)36°;(2)5.
【解析】试题分析:(1)、根据中垂线的性质得出∠ECD=∠A;(2)、根据等腰三角形的性质得出∠B=∠ACB=72°,然后得出∠BCE=36°,从而得出∠BEC=72°=∠B,然后得出答案.
试题解析:(1)、∵DE垂直平分AC, ∴CE=AE, ∴∠ECD=∠A=36°.
(2)、∵AB=AC,∠A=36°, ∴∠B=∠ACB=72°,∵∠ECD=36°,∴∠BCE=∠ACB﹣∠ECD=36°,
∠BEC=72°=∠B, ∴BC=EC=12.

练习册系列答案
相关题目