Question

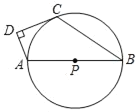
【题目】如图，已知AB是⊙P的直径，点C在⊙P上，D为⊙P外一点，且∠ADC＝90°，2∠B+∠DAB＝180°．

(1)证明：直线CD为⊙P的切线；

(2)若DC＝2，AD＝4，求⊙P的半径．

Answer 1

【答案】(1)证明见解析；(2)⊙P的半径为5．

【解析】

（1）连接PC，则∠APC＝2∠B，可证PC∥DA，证得PC⊥CD，则结论得证；

（2）连接AC，先求出AC长，可证△ADC∽△ACB，可求出AB长，则⊙P的半径可求出．

(1)连接PC，

∵PC＝PB，

∴∠B＝∠PCB，

∴∠APC＝2∠B，

∵2∠B+∠DAB＝180°，

∴∠DAC+∠ACP＝180°，

∴PC∥DA，

∵∠ADC＝90°，

∴∠DCP＝90°，

即DC⊥CP，

∴直线CD为⊙P的切线；

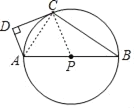
(2)连接AC，

∵DC＝，AD＝4，∠ADC＝90°，

∴，

∵AP＝CP，

∴∠PAC＝∠ACP，

∵AD∥PC，

∴∠DAC＝∠ACP，

∴∠PAC＝∠DAC，

∵AB是⊙P的直径，

∴∠BCA＝90°，

∴∠BCA＝∠ADC，

∴△ADC∽△ACB，

∴，

∴，

∴AB＝10，

∴⊙P的半径为5．