题目内容
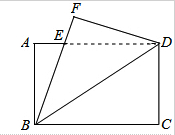 如图,将矩形ABCD沿对角线BD折叠,使点C落在点F处,且BF与AD相交于点E,若AD=8cm,AB=4cm,则AE=
如图,将矩形ABCD沿对角线BD折叠,使点C落在点F处,且BF与AD相交于点E,若AD=8cm,AB=4cm,则AE=3cm
3cm
.分析:先判断∠EDB=∠EBD,从而得出ED=EB,设AE=x,则可得出EB=ED=(8-x)cm,在RT△AEB中利用勾股定理即可得出x的值.
解答:解:由题意得,∠DBC=∠DBF,
∵AD∥BC,
∴∠EDB=∠DBC=∠EBD,
∴ED=EB,
设AE=xcm,则EB=ED=(8-x)cm,
在RT△AEB中,BE2=AE2+AB2,即(8-x)2=x2+42,
解得:x=3,即AE=3cm.
故答案为:3cm.
∵AD∥BC,
∴∠EDB=∠DBC=∠EBD,
∴ED=EB,
设AE=xcm,则EB=ED=(8-x)cm,
在RT△AEB中,BE2=AE2+AB2,即(8-x)2=x2+42,
解得:x=3,即AE=3cm.
故答案为:3cm.
点评:此题考查了翻折变换的性质及勾股定理的知识,解答本题的关键是根据题意得出ED=EB,这是解答本题的突破口.

练习册系列答案
相关题目
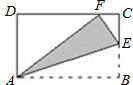 如图,将矩形ABCD的BC边折起,使点B落在DC上的点F处得折痕AE,若∠DFA为40°,则∠EAF的度数是( )
如图,将矩形ABCD的BC边折起,使点B落在DC上的点F处得折痕AE,若∠DFA为40°,则∠EAF的度数是( )| A、15° | B、20° | C、25° | D、30° |
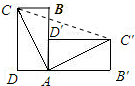 如图,将矩形ABCD绕点A顺时针旋转90°后,得到矩形AB′C′D′,如果CD=2DA=2,那么CC′=
如图,将矩形ABCD绕点A顺时针旋转90°后,得到矩形AB′C′D′,如果CD=2DA=2,那么CC′= 4、如图,将矩形ABCD折叠,AE是折痕,点D恰好落在BC边上的点F处,量得∠BAF=50°,那么∠DEA等于( )
4、如图,将矩形ABCD折叠,AE是折痕,点D恰好落在BC边上的点F处,量得∠BAF=50°,那么∠DEA等于( ) 12、如图,将矩形ABCD沿直线EF对折,点D恰好与BC边上的点H重合,∠GFP=62°,那么∠EHF的度数等于
12、如图,将矩形ABCD沿直线EF对折,点D恰好与BC边上的点H重合,∠GFP=62°,那么∠EHF的度数等于 如图,将矩形ABCD绕C点顺时针旋转到矩形CEFG,点E在CD上,若AB=8,BC=6,则旋转过程中点A所经过的路径长为
如图,将矩形ABCD绕C点顺时针旋转到矩形CEFG,点E在CD上,若AB=8,BC=6,则旋转过程中点A所经过的路径长为